题目内容
4.某农户买黄金瓜,第一天上午买了45斤,价格为每斤x元,下午他又买了35斤,价格为每斤y元.第二天他以每斤$\frac{x+y}{2}$元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )| A. | x<y | B. | x>y | C. | x≤y | D. | x≥y |
分析 根据题意,可得买黄瓜每斤的平均价>卖黄瓜每斤的平均价,然后根据单价=总价÷数量,用第一天买黄金瓜花的钱除以购买的斤数,求出买黄瓜每斤的平均价是多少,再根据买黄瓜每斤的平均价>卖黄瓜每斤的平均价,应用不等式的性质,判断出x、y的关系即可.
解答 解:根据题意,可得
买黄瓜每斤的平均价>卖黄瓜每斤的平均价,
∴(45x+35y)÷(45+35)>$\frac{x+y}{2}$,
∴(45x+35y)÷80>$\frac{x+y}{2}$,
∴(45x+35y)÷80×80>$\frac{x+y}{2}$×80,
∴45x+35y>40x+40y,
整理,可得
x>y.
故选:B.
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.

练习册系列答案
相关题目
16.下列运算和化简,不正确的是( )
| A. | $\sqrt{{{0.5}^2}}$=0.5 | B. | $\sqrt{\frac{4}{3}}=\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{8}×\sqrt{\frac{1}{2}}=2$ | D. | ${(-7\sqrt{\frac{2}{7}})^2}=7\frac{2}{7}$ |
 如图,在△ABC中,BC边上的高是AD.
如图,在△ABC中,BC边上的高是AD.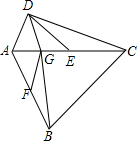 如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,
如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G, 如图,在△ABC中,AD为△ABC的中线,BE为△ABD的中线,若S△ABC=80,BD=8,则点E到BC边的距离为5.
如图,在△ABC中,AD为△ABC的中线,BE为△ABD的中线,若S△ABC=80,BD=8,则点E到BC边的距离为5.