题目内容
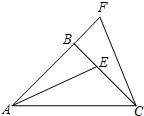 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF(1)求证:△ABE≌△CBF;
(2)若∠CAE=25°,求∠ACF的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)运用HL定理直接证明△ABE≌△CBF,即可解决问题.
(2)证明∠BAE=∠BCF=25°;求出∠ACB=45°,即可解决问题.
(2)证明∠BAE=∠BCF=25°;求出∠ACB=45°,即可解决问题.
解答: 解:(1)在Rt△ABE与Rt△CBF中,
解:(1)在Rt△ABE与Rt△CBF中,
,
∴△ABE≌△CBF(HL).
(2)∵△ABE≌△CBF,
∴∠BAE=∠BCF=25°;
∵AB=BC,∠ABC=90°,
∴∠ACB=45°,
∴∠ACF=70°.
 解:(1)在Rt△ABE与Rt△CBF中,
解:(1)在Rt△ABE与Rt△CBF中,
|
∴△ABE≌△CBF(HL).
(2)∵△ABE≌△CBF,
∴∠BAE=∠BCF=25°;
∵AB=BC,∠ABC=90°,
∴∠ACB=45°,
∴∠ACF=70°.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;准确找出图形中隐含的相等或全等关系是解题的关键.

练习册系列答案
相关题目
 如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小. (保留作图痕迹)
如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小. (保留作图痕迹)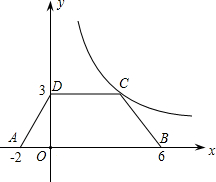 如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. 如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.
如图是由4个边长为1的正方形组成的图形,请求出∠ABC的度数.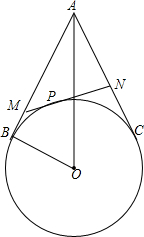 已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值. 找出图中互相垂直的线段,并用三角尺检验.
找出图中互相垂直的线段,并用三角尺检验. 如图所示为一矩形木框,四周为宽度相同的木条,那么这个矩形框的里、外两个矩形是相似形码?假设木框长为30cm,宽为20cm,木条的宽度为2cm,试加以验证.
如图所示为一矩形木框,四周为宽度相同的木条,那么这个矩形框的里、外两个矩形是相似形码?假设木框长为30cm,宽为20cm,木条的宽度为2cm,试加以验证.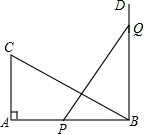 如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?
如图,Rt△ABC中,∠A=90°,AC=6,AB=8,BD⊥AB,P,Q分别为AB,BD上的动点且PQ=BC,点P在AB上的什么位置时,△PQB与△ABC全等?