题目内容
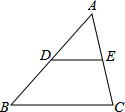如图，在△ABC中，D、E分别是AB、AC的中点，若△ABC的面积为 S△ABC=36cm2，则△ADE的面积S△ADE为（ ）| A、6 | B、9 | C、12 | D、18 |
考点：相似三角形的判定与性质
专题：
分析：直接利用三角形中位线定理得出DE
BC，即可得出△ADE∽△ABC，再利用相似三角形的性质求出答案．
| ∥ |
. |
| 1 |
| 2 |
解答：解：∵D、E分别是AB、AC的中点，
∴DE
BC，
∴△ADE∽△ABC，
∴
=
=
，
∴
=
，
∵△ABC的面积为 S△ABC=36cm2，
∴△ADE的面积S△ADE=9cm2．
故选：B．
∴DE
| ∥ |
. |
| 1 |
| 2 |
∴△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
| 1 |
| 2 |
∴
| S△ADE |
| S△ABC |
| 1 |
| 4 |
∵△ABC的面积为 S△ABC=36cm2，
∴△ADE的面积S△ADE=9cm2．
故选：B．
点评：此题主要考查了相似三角形的判定与性质，得出△ADE∽△ABC是解题关键．
练习册系列答案
相关题目
如图，在等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC
如图，梯形ABCD中，AD∥BC，对角线BD恰好平分∠ABC，那么图中可以证明一定相等的两条线段是（ ）| A、AB=CD |
| B、AD=CD |
| C、AB=AD |
| D、BD=BC |
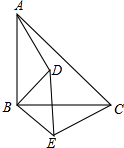已知：如图，△ABC和△DBE均为等腰直角三角形．
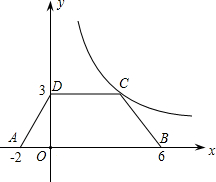如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（-2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC、AC于D、E两点，过点D作DE⊥AC，垂足为F．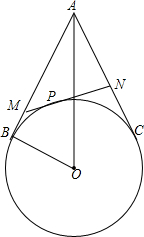
已知，如图，A是⊙O外一点，AB，AC分别与⊙O相切于点B，C，P是BC上任意一点，过点P作⊙O的切线，交AB于点M，交AC于点N，设AO=d，BO=r．求证：△AMN的周长是一个定值，并求出这个定值．
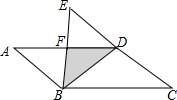如图，已知四边形ABCD是一张平行四边形纸片，BD是一条对角线，且BD⊥DC，现沿BD将纸片翻折，使C点到达E点．
如图所示，AB∥CD，∠A=∠F，∠D=∠E，求∠EOF的度数．