题目内容
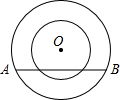 如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )
如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )| A、8≤AB≤10 |
| B、8<AB<10 |
| C、8<AB≤10 |
| D、6≤AB≤10 |
考点:直线与圆的位置关系
专题:
分析:此题可以首先计算出当AB与小圆相切的时候的弦长.连接过切点的半径和大圆的一条半径,根据勾股定理和垂径定理,得AB=8.若大圆的弦AB与小圆有两个公共点,即相交,此时AB>8;又因为大圆最长的弦是直径10,则8<AB≤10.
解答:解:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2
=8.
∵大圆的弦AB与小圆有两个公共点,即相交,
∴8<AB≤10.
故选C.
∵大圆半径为5,小圆的半径为3,
∴AB=2
| 52-32 |
∵大圆的弦AB与小圆有两个公共点,即相交,
∴8<AB≤10.
故选C.
点评:本题综合运用了切线的性质、勾股定理和垂径定理.此题可以首先计算出和小圆相切时的弦长,再进一步分析相交时的弦长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )
如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )| A、1:2 | B、2:3 |
| C、1:3 | D、1:4 |
 如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )
如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )| A、AB=CD |
| B、AD=CD |
| C、AB=AD |
| D、BD=BC |
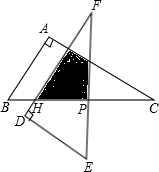 如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为
如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为 如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小. (保留作图痕迹)
如图,M,N分别为△ABC边AB,AC上的点,在BC边上求作一点P,使△MNP的周长最小. (保留作图痕迹)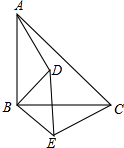 已知:如图,△ABC和△DBE均为等腰直角三角形.
已知:如图,△ABC和△DBE均为等腰直角三角形.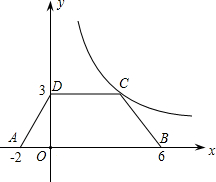 如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.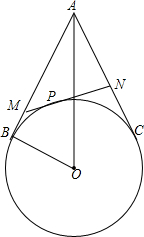 已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.