题目内容
6.已知△ABC与△A′B′C′,若AC=5,BC=12,AB=13,A′C′=10,B′C′=24.那么A′B′长度 是多少时,△ABC∽△A′B′C′?说明理由.分析 分两种情况讨论:①当A′B′为最长边时,由$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$=$\frac{1}{2}$,即可求出A′B′的长度;
②当B′C′为最长边时,$\frac{AB}{B′C′}$=$\frac{13}{24}$≠$\frac{AC}{A′C′}$,得出△ABC与△A′B′C′不相似;即可得出结果.
解答 解:A′B′=26时,△ABC∽△A′B′C′;理由如下:
分两种情况讨论:
①当A′B′为最长边时,
∵$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$=$\frac{1}{2}$,
∴当$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$=$\frac{1}{2}$时,△ABC∽△A′B′C′,
此时A′B′=2AB=26;
②当B′C′为最长边时,$\frac{AB}{B′C′}$=$\frac{13}{24}$≠$\frac{AC}{A′C′}$,
∴△ABC与△A′B′C′不相似;
综上所述:当A′B′=26时,△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,由三边成比例得出三角形相似是解决问题的关键,再由进行分类讨论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15. 如图,已知BC=6,AD垂直平分BC于点D,且AB=5,则△ABC的面积是( )
如图,已知BC=6,AD垂直平分BC于点D,且AB=5,则△ABC的面积是( )
 如图,已知BC=6,AD垂直平分BC于点D,且AB=5,则△ABC的面积是( )
如图,已知BC=6,AD垂直平分BC于点D,且AB=5,则△ABC的面积是( )| A. | 24 | B. | 12 | C. | 6 | D. | 3 |
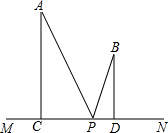 点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.
点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.