题目内容
1.(1)如图1①,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠BAC=40°,求∠AMB的度数;(2)如图1②,如果将(1)中的∠BAC的度数改为70°,其余条件不变,再求∠AMB的度数.
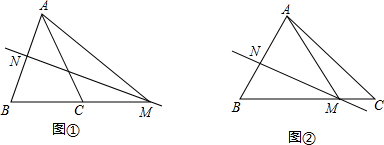
分析 (1)由在△ABC中,AB=AC,∠A=40°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AB于点N,交BC的延长线于点M,即可求得答案;
(2)由在△ABC中,AB=AC,∠A=70°,根据等腰三角形的性质,可求得∠ABC的度数,又由AB的垂直平分线交AB于点N,交BC的延长线于点M,即可求得答案.
解答 解:∵∠ABC=∠ACB,∠BAC=40°,
∴∠ABC=70°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴AM=BM,
∴∠BAM=∠ABC=70°,
∴∠AMB=180°-∠ABC-∠BAM=40°;
(2)∵∠ABC=∠ACB,∠BAC=70°,
∴∠ABC=55°,
∵AB的垂直平分线交AB于点N,交BC的延长线于点M,
∴AM=BM,
∴∠BAM=∠ABC=55°,
∴∠AMB=180°-∠ABC-∠BAM=70°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
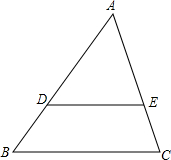 如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.
如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.