题目内容
16．求|x-1|+|x-2|+|x-3|+|x-4|+…+|x-101|的最小值．分析 当绝对值的个数为奇数时，取得最小值x是其中间项，而当绝对值的个数为偶数时，则x取中间两项结果一样．从而得出对于|x-1|+|x-2|+|x-3|+…+|x-101|，当x=51时取得最小值．
解答 解：由绝对值的几何意义可知，当绝对值的个数为奇数时，取得最小值x是其中间项，而当绝对值的个数为偶数时，则x取中间两项结果一样．
因此，对于|x-1|+|x-2|+|x-3|+…+|x-101|，当x=51时取得最小值，
此时原式=50+49+…+0+1+2+…+49+50=50×（1+50）=2550．
点评 此题主要考查了绝对值，培养学生运算求解能力，归纳能力，属于基础题．
练习册系列答案
相关题目
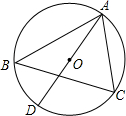如图，△ABC是⊙O内接三角形，AD是⊙O的直径，AD=6，∠ABC=∠CAD，求弦AC所对的弧长．
某学校为了改善教职工居住条件，准备在教学楼的正南方建筑一栋住宅楼．要求教学楼与住宅楼等高．均为15.6m．已知该地区冬至正午时分太阳高度最低，太阳光线与水平线的夹角为30°，教学楼与住宅楼相距19.2m，如图所示，