题目内容
17.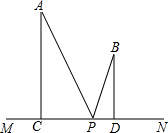 点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.
点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=5,已知CD=4,P是直线MN上的一个动点,记PA+PB的最小值为a,|PA-PB|的最大值为b,求a2-b2的值.
分析 作点A关于直线L的对称点A′,连接A′B交直线L于点P,过点A′作直线A′E⊥BD的延长线于点E,再根据勾股定理求出A′B的长就是PA+PB的最小值;
延长AB交MN于点P′,此时P′A-P′B=AB,由三角形三边关系可知AB>|PA-PB|,故当点P运动到P′点时|PA-PB|最大,作BE⊥AM,由勾股定理即可求出AB的长就是|PA-PB|的最大值.进一步代入求得答案即可.
解答 解:如图,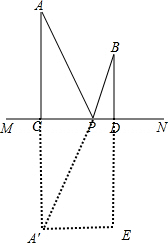
作点A关于直线L的对称点A′,连接A′B交直线L于点P,
则点P即为所求点.
过点A′作直线AE⊥BD的延长线于点E,则线段A′B的长即为PA+PB的最小值.
∵AC=8cm,BD=5cm,CD=4cm,
∴A′C=8cm,BE=8+5=13cm,A′E=CD=4cm,
∴A′B=$\sqrt{1{3}^{2}+{4}^{2}}$=$\sqrt{185}$,
即PA+PB的最小值是a=$\sqrt{185}$.
如图,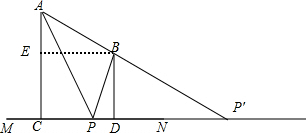
延长AB交MN于点P′,
∵P′A-P′B=AB,AB>|PA-PB|,
∴当点P运动到P′点时,|PA-PB|最大,
∵BD=5,CD=4,AC=8,
过点B作BE⊥AC,则BE=CD=4,AE=AC-BD=8-5=3,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5.
∴|PA-PB|=5为最大,
即b=5,
∴a2-b2=185-25=160.
点评 本题考查的是最短线路问题及勾股定理,熟知两点之间线段最短及三角形的三边关系是解答此类问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
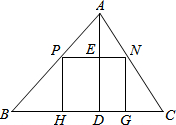 如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?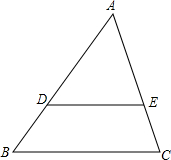 如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.
如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由. 如图所示,在Rt△ABC中,已知∠B=90°,∠C=30°,AB=1,求$\frac{AB}{AC}$•$\frac{AB}{BC}$•$\frac{BC}{AC}$的值.
如图所示,在Rt△ABC中,已知∠B=90°,∠C=30°,AB=1,求$\frac{AB}{AC}$•$\frac{AB}{BC}$•$\frac{BC}{AC}$的值.