题目内容
1.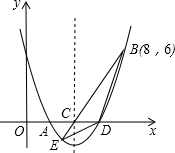 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,直接写出△BDE的面积.
分析 (1)把A(2,0),B(8,6)代入y=$\frac{1}{2}$x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)先把(1)中的解析式配成顶点式即可得到顶点坐标,然后利用抛物线对称性确定D点坐标;
(3)先利用待定系数法求出直线BC的解析式,再利用解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=\frac{1}{2}{x}^{2}-4x+6}\end{array}\right.$得E点坐标,然后利用S△BDE=S△BDC+S△EDC进行计算即可.
解答 解:(1)把A(2,0),B(8,6)代入y=$\frac{1}{2}$x2+bx+c得$\left\{\begin{array}{l}{\frac{1}{2}×4+2b+c=0}\\{\frac{1}{2}×64+8b+c=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-4}\\{c=6}\end{array}\right.$,
所以二次函数解析式为y=$\frac{1}{2}$x2-4x+6;
(2)y=$\frac{1}{2}$x2-4x+6=$\frac{1}{2}$(x-4)2-2,
所以二次函数图象的顶点坐标为(4,-2),
由于抛物线的对称轴为直线x=4,而A(2,0),
所以D点坐标为(6,0);
(3)C(4,0),
设直线BC的解析式为y=mx+n,
把B(8,6),C(4,0)代入得$\left\{\begin{array}{l}{8m+n=6}\\{4m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=-6}\end{array}\right.$,
所以直线BC的解析式为y=$\frac{3}{2}$x-6,
解方程组$\left\{\begin{array}{l}{y=\frac{3}{2}x-6}\\{y=\frac{1}{2}{x}^{2}-4x+6}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-\frac{3}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=8}\\{y=6}\end{array}\right.$,
所以E点坐标为(3,-$\frac{3}{2}$),
所以S△BDE=S△BDC+S△EDC=$\frac{1}{2}$×(6-4)×6+$\frac{1}{2}$×(6-4)×$\frac{3}{2}$=$\frac{15}{2}$.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质和三角形面积公式.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案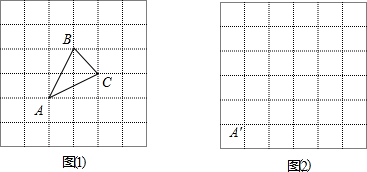
 小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.
小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.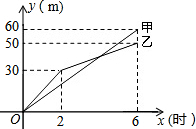 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: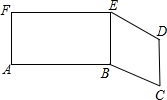 如图,有一张纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你画一条直线把这张纸片分成面积相等的两部分,并说明理由.
如图,有一张纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你画一条直线把这张纸片分成面积相等的两部分,并说明理由. 某厂有一块如图所示的△ABC铜板,根据需要,现要把它加工成一个平行四边形铜板,要把材料完全利用起来,可怎样加工?请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形,能否将此三角形铜板加工成长方形?请给出说明.
某厂有一块如图所示的△ABC铜板,根据需要,现要把它加工成一个平行四边形铜板,要把材料完全利用起来,可怎样加工?请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形,能否将此三角形铜板加工成长方形?请给出说明. 如图,在?ABCD中,已知AB=4cm,BC=9cm,∠B=30°,求?ABCD的面积.
如图,在?ABCD中,已知AB=4cm,BC=9cm,∠B=30°,求?ABCD的面积.