题目内容
16.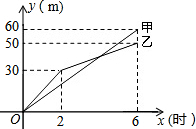 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:(1)求乙队在0≤x≤2的时段内的施工速度;
(2)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(3)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
分析 (1)由图可知,乙队在0≤x≤2的时段内2小时施工30米,根据速度=路程÷时间,即可解答;
(2)设函数关系式为y=kx+b,然后利用待定系数法求一次函数解析式解答;
(3)先求出甲队的速度,然后设甲队从开始到完工所铺设彩色道砖的长度为z米,再根据6小时后两队的施工时间相等列出方程求解即可.
解答 解:(1)乙队在0≤x≤2的时段内的施工速度为:30÷2=15米/时;
(2)设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b,
由图可知,函数图象过点(2,30),(6,50),
∴$\left\{\begin{array}{l}{2k+b=30}\\{6k+b=50}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=5}\\{b=20}\end{array}\right.$,
∴y=5x+20;
(3)由图可知,甲队速度是:60÷6=10(米/时),
设甲队从开始到完工所铺设彩色道砖的长度为z米,
依题意,得$\frac{z-60}{10}=\frac{z-50}{12}$,
解得z=110,
答:甲队从开始到完工所铺设彩色道砖的长度为110米.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,难点在于(3)根据6小时后的施工时间相等列出方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
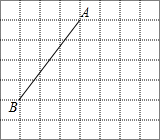 线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
线段AB的端点在边长为1的正方形网格格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.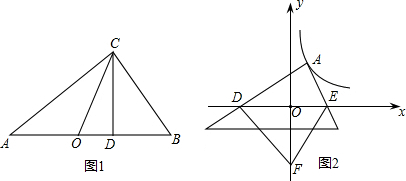
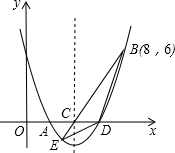 如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
如图,二次函数y=$\frac{1}{2}$x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).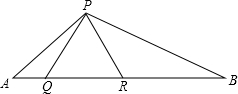 如图所示,已知△PQR是等边三角形,∠APB=120°.
如图所示,已知△PQR是等边三角形,∠APB=120°.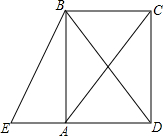 如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.
如图,四边形ABCD是矩形,延长DA至点E,使得AC=BE.