题目内容
11.在平面直角坐标系中,将抛物线y=x2先向右平移4个单位,再向上平移3个单位,得到抛物线L,则抛物线L的解析式为y=(x-4)2+3.分析 先利用顶点式得到抛物线y=x2的顶点坐标为(0,0),再利用点平移的坐标规律得到点(0,0)平移后所得对应点的坐标为(4,3),然后利用顶点式写出平移后得到的抛物线的解析式.
解答 解:抛物线y=x2的顶点坐标为(0,0),点(0,0)向右平移4个单位,再向上平移3个单位所得对应点的坐标为(4,3),所以平移后的抛物线L的解析式为y=(x-4)2+3.
故答案为y=(x-4)2+3.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| B. | “购买1张彩票就中奖”是不可能事件 | |
| C. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| D. | 甲、乙两组数据,若${{S}_{甲}}^{2}$>${{S}_{乙}}^{2}$,则乙组数据离散程度大 |
6.把抛物线y=x2-3向右平移2个单位,然后向上平移2个单位,则平移后得到的抛物线的解析式为( )
| A. | y=(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x+2)2+1 |
1.有五张正面分别写有数字-3,-2,1,2,3的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为a的值,然后再从剩余的四张卡片中随机抽取一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
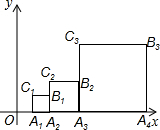 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).