题目内容
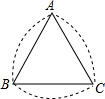如图所示的曲边三角形可按下述方法作出：作等边三角形ABC；分别以点A，B，C为圆心，以AB的长为半径作 |
| BC |
|
| AC |
|
| AB |
考点：扇形面积的计算
专题：
分析：此三角形是由三段弧组成，如果周长为π，则其中的一段弧长就是
，所以根据弧长公式可得
=
，解得r=1，即正三角形的边长为1．那么曲边三角形的面积就=三角形的面积+三个弓形的面积．
| π |
| 3 |
| 60π×r |
| 180 |
| π |
| 3 |
解答：解：1×
÷2+（
-
）×3=
．
| ||
| 2 |
| 60π×1 |
| 360 |
| ||
| 4 |
π-
| ||
| 2 |
点评：本题考查了扇形面积的计算．此题的关键是明确曲边三角形的面积就=三角形的面积+三个弓形的面积，然后再根据所给的曲线三角形的周长求出三角形的边长，从而求值．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
如图，AB⊥BD，ED⊥BD，C是BD上的一点，BC=DE，AB=CD．求证：AC⊥CE．若⊙O的面积为25π，在同一平面内有一个点P，且点P到圆心O的距离为4.9，则点P与⊙O的位置关系为（ ）
| A、点P在⊙O外 |
| B、点P在⊙O上 |
| C、点P在⊙O内 |
| D、无法确定 |
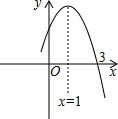若y=ax2+bx+c的部分图象如图所示，则关于x的方程ax2+bx+c=0的另一个解为（ ）| A、-2 | B、-1 | C、0 | D、1 |
