题目内容
10.a,b,c不全为0,满足a+b+c=0,a3+b3+c3=0,称使得an+bn+cn=0恒成立的正整数n为“好数”,则不超过2007的正整数中“好数”的个数为( )| A. | 2 | B. | 1004 | C. | 2006 | D. | 2007 |
分析 首先得到a3+b3+c3=(a+b+c)(a2+b2+c2-ab-bc-ca)+3abc,根据a+b+c=0,a3+b3+c3=0得到3abc=0,从而根据a、b、c不全为零得到a、b、c中只有一个数为零,最终确定奇数满足条件,从而确定前2007个整数中奇数的个数即可确定好数的个数.
解答 解:a3+b3+c3=(a+b+c)(a2+b2+c2-ab-bc-ca)+3abc
∵a+b+c=0,a3+b3+c3=0,
∴3abc=0,
∵a、b、c不全为零,
∴a、b、c中只有一个数为零,
不妨设c=0,从而a=-b,
∴此an+bn+cn=0恒成立即(-b)n+bn=0恒成立,
∴显然满足条件的正整数n为奇数,
即不超过2007的正整数中“好数”有1、3、5、…、2007共1004个,
故选B.
点评 本题考查了整数问题的综合运用,解题的关键是能够根据题意确定所有的奇数满足条件,难度中等.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
20.下列叙述正确的是( )
| A. | 方差越大,说明数据就越稳定 | |
| B. | 在不等式两边同乘或同除以一个不为0的数时,不等号的方向不变 | |
| C. | 对角线垂直的平行四边形是菱形 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
1.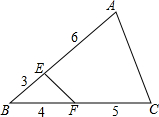 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )| A. | 4:23 | B. | 4:25 | C. | 5:26 | D. | 1:6 |
18.$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为( )
| A. | 1 | B. | $\frac{{2}^{n-2}}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n}}$ | D. | $\frac{{2}^{n}-1}{2n}$ |
5. 如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
 如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
15.一个商人将99颗弹子放进两个盒子,每个大盒子装12个,每个小盒子装5个,恰好装完.盒子总个数大于9,问大小盒子各几个?( )
| A. | 大的2个,小的15个 | |
| B. | 大的7个,小的3个 | |
| C. | 大的2个,小的15个或 大的7个,小的3个 | |
| D. | 无数种 |
2.x是不大于5的正数,则下列表示正确的是( )
| A. | 0<x<5 | B. | 0<x≤5 | C. | 0≤x≤5 | D. | x≤5 |
20. 如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )
如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )
 如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )
如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分∠BCD,∠A=65°,∠ABC=85°,则△BCD是( )| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |