题目内容
11. 如图所示,将△ABC绕点A按逆时针旋转50°后,得到△ADC′,则∠ABD的度数是( )
如图所示,将△ABC绕点A按逆时针旋转50°后,得到△ADC′,则∠ABD的度数是( )| A. | 30° | B. | 45° | C. | 65° | D. | 75° |
分析 先根据旋转的性质得AB=AD,∠BAD=50°,则利用等腰三角形的性质得到∠ABD=∠ADB,然后根据三角形内角和计算∠ABD的度数.
解答 解:∵△ABC绕点A按逆时针旋转50°后,得到△ADC′,
∴AB=AD,∠BAD=50°,
∴∠ABD=∠ADB,
∴∠ABD=$\frac{1}{2}$(180°-50°)=65°.
故选C.
点评 本题考查了旋转的性质、等腰三角形的性质、三角形内角和定理;熟练掌握旋转的性质,得到△ABD为等腰三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.观察下列图形规律:当n=( )时,图形“•”的个数和“△”的个数相等

| A. | 9 | B. | 7 | C. | 6 | D. | 5 |
16. 如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )| A. | 115° | B. | 125° | C. | 120° | D. | 145° |
3. 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
 如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )
如图,已知圆心角∠BOC=100°,则圆周角∠BAC的大小是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
20.某校举行“我爱我校”演讲比赛,由7名学生组成评委组.小明统计了每位评委对某参赛选手的评分并制成如下表格:
如果以去掉一个最高分和一个最低分后其他5名评委的平均分记为选手的最后得分,那么表中的数据一定不发生变化的是( )
| 众数 | 中位数 | 平均数 | 方差 |
| 7.9 | 8.3 | 8.2 | 0.3 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
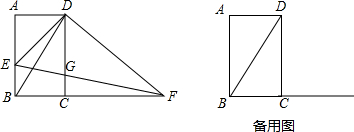
 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为5.5秒或14.5秒.
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为5.5秒或14.5秒.