题目内容
用指定的方法解方程:
(1)x2-6x=15(用配方法)
(2)(2x-1)2=3(2x-1)(用分解因式法)
(3)2x2-4x-1=0(用公式法)
(1)x2-6x=15(用配方法)
(2)(2x-1)2=3(2x-1)(用分解因式法)
(3)2x2-4x-1=0(用公式法)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)先配方得到(x-3)2=24,然后开平方解方程即可;
(2)先提取公因式(2x-1)得到(2x-1)(2x-1-3)=0,然后解一元一次方程即可;
(3)先找出a=2,b=-4,c=-1,然后代入公式求出方程的解.
(2)先提取公因式(2x-1)得到(2x-1)(2x-1-3)=0,然后解一元一次方程即可;
(3)先找出a=2,b=-4,c=-1,然后代入公式求出方程的解.
解答:
解:(1)∵x2-6x=15,
∴x2-6x+9=24,
∴(x-3)2=24,
∴x-3=±
,
∴x1=3+2
,x2=3-2
;
(2)∵(2x-1)2=3(2x-1),
∴(2x-1)(2x-1-3)=0,
∴2x-1=0,2x-4=0,
∴x1=
,x2=2;
(3)∵2x2-4x-1=0,
∴a=2,b=-4,c=-1,b2-4ac=24,
∴x=
,
∴x1=1+
,x2=1-
.
∴x2-6x+9=24,
∴(x-3)2=24,
∴x-3=±
| 24 |
∴x1=3+2
| 6 |
| 6 |
(2)∵(2x-1)2=3(2x-1),
∴(2x-1)(2x-1-3)=0,
∴2x-1=0,2x-4=0,
∴x1=
| 1 |
| 2 |
(3)∵2x2-4x-1=0,
∴a=2,b=-4,c=-1,b2-4ac=24,
∴x=
-(-4)±
| ||
| 2×2 |
∴x1=1+
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了因式分解法、配方法和公式法解一元二次方程的知识,解答本题的关键是熟练掌握因式分解法、配方法、公式法解一元二次方程过程和步骤,此题难度不大.

练习册系列答案
相关题目
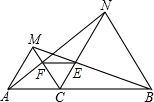 如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
 如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数.
如图,在△ABC中,∠C=90°,点E是斜边AB的中点,DE⊥AB,且∠CAD:∠BAD=5:2,求∠BAC的度数. 如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为
如图,把边长为5cm的正方形ABCD先向右平移a cm,再向上平移b cm(a、b均小于5),得到正方形EFGH,阴影部分的面积为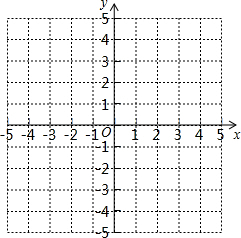 已知:点A(3,4),B(-2,3),C(1,0)
已知:点A(3,4),B(-2,3),C(1,0)