题目内容
已知二次函数y=
x2+kx+k-
.
(1)求证:不论k为任何实数,该二次函数的图象与x轴总有公共点;
(2)若该二次函数的图象与x轴有两个公共点A,B,且A点坐标为(3,0),求B点坐标.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求证:不论k为任何实数,该二次函数的图象与x轴总有公共点;
(2)若该二次函数的图象与x轴有两个公共点A,B,且A点坐标为(3,0),求B点坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)令y=0得到关于x的一元二次方程,再用k表示出该方程的判别式,可判断出其根的情况,可证得结论;
(2)把A点坐标代入可求得抛物线的解析式,再令y=0,可求得方程的解,可得出B点坐标.
(2)把A点坐标代入可求得抛物线的解析式,再令y=0,可求得方程的解,可得出B点坐标.
解答:
(1)证明:令y=0可得
x2+kx+k-
=0,
∵△=k2-4×
×(k-
)=k2-2k+1=(k-1)2≥0,
∴不论k为任何实数,方程
x2+kx+k-
=0总有实数根,
∴二次函数y=
x2+kx+k-
的图象与x轴总有公共点;
(2)解:∵A(3,0)在抛物线y=
x2+kx+k-
上,
∴
×32+3k+k-
=0,解得k=-1,
∴二次函数的解析式为y=
x2-x-
,
令y=0,即
x2-x-
=0,解得x=3或x=-1,
∴B点坐标为(-1,0).
| 1 |
| 2 |
| 1 |
| 2 |
∵△=k2-4×
| 1 |
| 2 |
| 1 |
| 2 |
∴不论k为任何实数,方程
| 1 |
| 2 |
| 1 |
| 2 |
∴二次函数y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:∵A(3,0)在抛物线y=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴二次函数的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,即
| 1 |
| 2 |
| 3 |
| 2 |
∴B点坐标为(-1,0).
点评:本题主要考查二次函数与方程的关系,掌握二次函数图象与x轴的交点横坐标为对应一元二次方程的两根是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
若有理数x的相反数是8,则x为( )
| A、-8 | ||
| B、8 | ||
C、-
| ||
D、
|
在数轴上,0为原点,某点A移动到B,移动了12.6个单位长度;点A表示数a,点B表示数b,且a+b=0,A到0的距离为( )
| A、12.6 | B、6.3 |
| C、-12.6 | D、-6.3 |
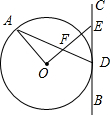 如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.
如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.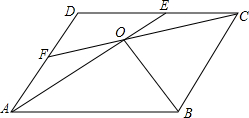 如图,在平行四边形ABCD中,AE=CF,求证:∠AOB=∠COB.
如图,在平行四边形ABCD中,AE=CF,求证:∠AOB=∠COB.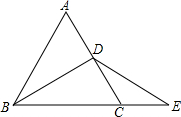 如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为
如图,在等边三角形ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为6cm,则△DCE的周长为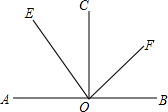 如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.
如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.