题目内容
18.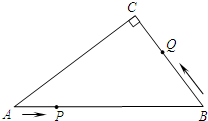 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
分析 分两种情况讨论,当∠BQP=90°时,则∠BPQ=30°,BP=2BQ,当∠QPB=90°时,BQ=2BP,再分别列出方程求解即可.
解答 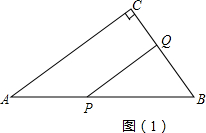 解:①如图(1),当∠BQP=90°时,则∠BPQ=30°,BP=2BQ,
解:①如图(1),当∠BQP=90°时,则∠BPQ=30°,BP=2BQ,
∵BP=12-3t,BQ=t,
∴12-3t=2t,
解得:t=$\frac{12}{5}$;
②如图(2)当∠QPB=90°时,
∵∠B=60°,
∴∠BQP=30°,
∴BQ=2BP,
若0<t<4,
则t=2(12-3t).
t=$\frac{24}{7}$,
若4<t≤6时,
则t=2(3t-12),
t=$\frac{24}{5}$;
故答案为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
点评 此题考查了勾股定理的逆定理,用到的知识点是直角三角形中,30度角所对的直角边是斜边的一半,关键是根据题意画出图形,注意分类讨论.

练习册系列答案
相关题目
9.抛物线y=-2x2-3与双曲线y=-$\frac{1}{x}$的交点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
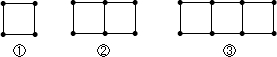
6. 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
 如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.| A. | 400 | B. | 500 | C. | 300 | D. | 750 |
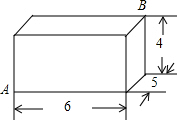 如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm.
如图,有一个长方体盒子,长、宽、高分别为6cm、5cm、4cm,有一只小虫要从点A处沿长方体表面爬到点B处,最短的路径长为$\sqrt{117}$cm.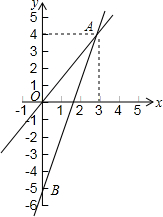 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.