题目内容
3.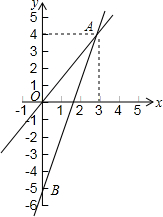 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB.(1)求这两个函数的关系式;
(2)两直线与x轴围成的三角形的面积.
分析 (1)设正比例函数是y=mx,设一次函数是y=kx+b.根据它们交于点A(4,3),得到关于m的方程和关于k、b的方程,从而首先求得m的值;根据勾股定理求得OA的长,从而得到OB的长,即可求得b的值,再进一步求得k值.
(2)求出点D的坐标,即可得出结果.
解答 解:(1)设正比例函数是y=mx,设一次函数是y=kx+b.
把A(4,3)代入y=mx得:4m=3,即m=$\frac{3}{4}$.
则正比例函数是y=$\frac{3}{4}$x;
把(4,3)代入y=kx+b,
得:4k+b=3①.
∵A(4,3),
∴根据勾股定理得OA=$\sqrt{{4}^{2}+{3}^{1}}$=5,
∴OB=OA=5,
∴b=-5.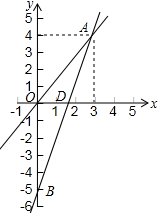
把b=-5代入①,得k=2.
则一次函数解析式是y=2x-5.
(2)设直线AB交x轴于D,如图所示:
对于y=2x-5,当y=0时,x=2.5,
则D(2.5,0),
两直线与x轴围成△AOD的面积=$\frac{1}{2}$×2.5×3=3.75.
点评 本题主要考查了用待定系数法求函数解析式和一次函数图象的性质、勾股定理、三角形面积的计算;熟练掌握用待定系数法求函数解析式是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.食品厂从生产的袋张食品中抽样20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正,负数表示,记录如下:
(1)20袋样本总质量比标准20袋总质量多还是少?多或少多少?
(2)若标准标明要求是450±2g为合格,则抽样检测的合格率是多少?
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 2 | 3 | 7 |
| 袋数 | 3 | 5 | 3 | 2 | 5 | 2 |
(2)若标准标明要求是450±2g为合格,则抽样检测的合格率是多少?
12. 如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
 如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )| A. | $2\sqrt{2}-2$ | B. | $2\sqrt{2}+2$ | C. | 2 | D. | $1+\sqrt{2}$ |
 如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4.
如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4.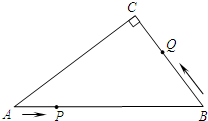 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.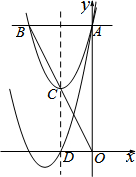 如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.
如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.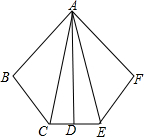 如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.
如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.