题目内容
8.用火柴棒按下图的方式搭图形: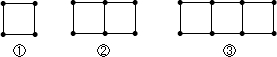
(1)①有4根火柴棒;图②有7根火柴棒;图③有10根火柴棒.
(2)按上面的方法继续下去,第100个图形中有多少根火柴棒?
(3)第n(n≥1的整数)个图形中有多少根火柴棒?
分析 (1)根据图形直接数出火柴棒的根数即可;
(2)根据图形的变化规律找到火柴根数的通项公式,代入n=100即可;
(3)根据(2)直接写出答案即可.
解答 解:(1)①有4根火柴棒;图②有7根火柴棒;图③有10根火柴棒,
故答案为:4,7,10;
(2)观察图形发现第一个图形有3+1=4根火柴棒;
第二个图形有3+3+1个火柴棒;
第三个图形有3+3+3+1根火柴棒;
…
第n个图形有3n+1根火柴棒;
当n=100时,3×100+1=301根火柴棒;
(3)由(2)得第n(n≥1的整数)个图形中有3n+1根火柴棒.
点评 本题考查了图形的变化类问题,解题的关键是了解图形的变化规律,利用规律得到火柴根数的通项公式,从而确定答案.

练习册系列答案
相关题目
16.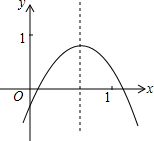 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
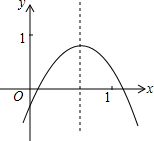 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | abc>0 | C. | a+b+c<0 | D. | b2-4ac<0 |
3.抛物线y=-(x+5)2-4的顶点坐标是( )
| A. | (5,4) | B. | (-5,4) | C. | (5,-4) | D. | (-5,-4) |
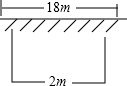 如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,
如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米, 如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4.
如图是正方体的展开图,则正方体中与数字5所在面相对的面上的数字为4. 如图,△ABC中,AD⊥BC于D,E在BC上,F在BA延长线上,CE=2BD,EF=AC
如图,△ABC中,AD⊥BC于D,E在BC上,F在BA延长线上,CE=2BD,EF=AC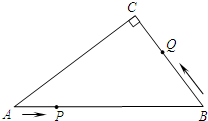 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为$\frac{12}{5}$、$\frac{24}{7}$、$\frac{24}{5}$.