题目内容
关于函数y=kx+b（k，b都是不等于0的常数），下列说法，正确的是（ ）
| A、y与x成正比例 |
| B、y与kx成正比例 |
| C、y与x+b成正比例 |
| D、y-b与x成正比例 |
考点：正比例函数的定义
专题：
分析：根据一般地，形如y=kx（k是常数，k≠0）的函数叫做正比例函数，其中k叫做比例系数，直接将原式变形进而得出y-b与x的关系．
解答：解：∵关于函数y=kx+b（k，b都是不等于0的常数），
∴y-b=kx，
∴y-b与x成正比例．
故选：D．
∴y-b=kx，
∴y-b与x成正比例．
故选：D．
点评：此题主要考查了正比例函数的定义，正确把握比例函数定义是解题关键．
练习册系列答案
相关题目
在△ABC中，AB=5cm，BC=6cm，BC边上的中线AD=4cm，则∠ADC的度数是（ ）
| A、60° | B、90° |
| C、120° | D、150° |
下面说法中，正确的是（ ）
| A、有一个角是直角的四边形是矩形 |
| B、两条对角线相等的四边形是矩形 |
| C、两条对角线互相垂直的四边形是矩形 |
| D、四个角都是直角的四边形是矩形 |
有50个数，它们的平均数为45，将其中的两个数12和30舍去，则余下数的平均数为（ ）
| A、46 | B、45 | C、50 | D、43 |
已知从一个多边形的一个顶点只可引出三条对角线，那么这个多边形是（ ）
| A、五边形 | B、六边形 |
| C、七边形 | D、八边形 |
方程（m-2）（m-3）x2-（m-2）（m+3）x+（m-2）=0是关于x的一元二次方程，则（ ）
| A、m≠3 |
| B、m≠2且m≠3 |
| C、m≠2 |
| D、m≠2且m≠-3 |
计算（5
+
-6
）÷
的值为（ ）
| 48 |
| 12 |
| 27 |
| 3 |
| A、4 | B、-4 | C、2 | D、-2 |
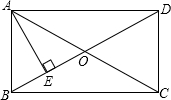如图，在矩形ABCD中，对角线AC、BD相交于点O，过点A作AE⊥BD，垂足为点E，若ED=3EO，AE=