题目内容
(1)直线y=kx+6与y轴的交点的坐标是什么?
(2)直线y=kx+6与x轴的交点的坐标是什么?(用含k的代数式表示出来)
(3)若直线y=kx+6与两坐标轴所围成的三角形面积是24,试求常数k的值.
(2)直线y=kx+6与x轴的交点的坐标是什么?(用含k的代数式表示出来)
(3)若直线y=kx+6与两坐标轴所围成的三角形面积是24,试求常数k的值.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:(1)直线与y轴交点的横坐标等于零,所以把x=0代入函数解析式来求相应的y值;
(2)直线与x轴的交点的纵坐标等于零,所以把y=0代入函数解析式来求相应的x的值;
(3)根据三角形的面积公式即可得出结论.
(2)直线与x轴的交点的纵坐标等于零,所以把y=0代入函数解析式来求相应的x的值;
(3)根据三角形的面积公式即可得出结论.
解答:解:(1)把x=0代入y=kx+6,得
y=6,
所以直线y=kx+6与y轴的交点的坐标是(0,6);
(2)把y=0代入y=kx+6,得
kx+6=0,
解得,x=-
,
所以直线y=kx+6与x轴的交点的坐标是(-
,0);
(3)解:∵直线y=kx+6与坐标轴的交点分别为(0,6),(-
,0),
∴S=
×|-
|×6=24,解得k=±
.
所以求常数k的值的是±
.
y=6,
所以直线y=kx+6与y轴的交点的坐标是(0,6);
(2)把y=0代入y=kx+6,得
kx+6=0,
解得,x=-
| 6 |
| k |
所以直线y=kx+6与x轴的交点的坐标是(-
| 6 |
| k |
(3)解:∵直线y=kx+6与坐标轴的交点分别为(0,6),(-
| 6 |
| k |
∴S=
| 1 |
| 2 |
| 6 |
| k |
| 3 |
| 4 |
所以求常数k的值的是±
| 3 |
| 4 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
下面说法中,正确的是( )
| A、有一个角是直角的四边形是矩形 |
| B、两条对角线相等的四边形是矩形 |
| C、两条对角线互相垂直的四边形是矩形 |
| D、四个角都是直角的四边形是矩形 |
计算(5
+
-6
)÷
的值为( )
| 48 |
| 12 |
| 27 |
| 3 |
| A、4 | B、-4 | C、2 | D、-2 |
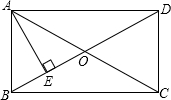 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE= 某工厂要制作符合条件的模板,如图,要∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测∠BDC的度数的方法筛选出不合格的产品,若测∠BDC的度数为150°,则这种模板是否合格?请说明理由.
某工厂要制作符合条件的模板,如图,要∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测∠BDC的度数的方法筛选出不合格的产品,若测∠BDC的度数为150°,则这种模板是否合格?请说明理由. 线段HB上一动点,以E为圆心,EA为半径作⊙E,⊙E与线段DC相交于点F,设AE=x,DF=y,
线段HB上一动点,以E为圆心,EA为半径作⊙E,⊙E与线段DC相交于点F,设AE=x,DF=y,