题目内容
 如图,将△ABC的边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD;再将边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,试问:
如图,将△ABC的边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD;再将边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,试问:(1)E点和D点重合吗?
(2)如果(1)成立,那么∠B和∠ADC相等吗?为什么?
考点:平移的性质
专题:几何图形问题
分析:(1)根据一组对边平行且相等的四边形是平行四边形判断出四边形ABCD是平行四边形,再根据平行四边形的性质可得CD∥AB,CD=AB,然后根据平移的性质,CE∥AB,CE=AB,从而得到点E、D重合;
(2)根据平行四边形的对角相等解答.
(2)根据平行四边形的对角相等解答.
解答:解:(1)点E、D重合.
理由如下:∵边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD,
∴BC∥AD,BC=AD,
∴四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∵边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,
∴CE∥AB,CE=AB,
∴点E、D重合;
(2)∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
理由如下:∵边BC沿射线BA方向平移,距离为线段AB的长,得到线段AD,
∴BC∥AD,BC=AD,
∴四边形ABCD是平行四边形,
∴CD∥AB,CD=AB,
∵边AB沿BC方向平移,平移的距离为线段BC的长,得到线段CE,
∴CE∥AB,CE=AB,
∴点E、D重合;
(2)∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
点评:本题考查了平移的性质,熟记性质并判断出四边形ABCD是平行四边形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
若最简二次根式
和
能合并,则x的值可能为( )
| 2x+1 |
| 4x-3 |
A、-
| ||
B、
| ||
| C、2 | ||
| D、5 |
方程(m-2)(m-3)x2-(m-2)(m+3)x+(m-2)=0是关于x的一元二次方程,则( )
| A、m≠3 |
| B、m≠2且m≠3 |
| C、m≠2 |
| D、m≠2且m≠-3 |
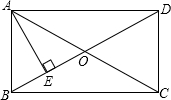 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=