题目内容
若m2+m-1=0,求m4+2m3-m-2009的值.
考点:因式分解的应用
专题:计算题,因式分解
分析:观察已知m2+m-1=0可转化为m2+m=1,再对m4+2m3-m-2009提取公因式因式分解的过程中将m2+m作为一个整体代入,逐次降低m的次数,使问题得以解决.
解答:解:∵m2+m-1=0
∴m2+m=1
∴m4+2m3-m-2009
=m2(m2+m)+m3-m-2009
=m2+m3-m-2009
=m(m2+m)-m-2009
=m-m-2009
=-2009.
∴m2+m=1
∴m4+2m3-m-2009
=m2(m2+m)+m3-m-2009
=m2+m3-m-2009
=m(m2+m)-m-2009
=m-m-2009
=-2009.
点评:此题考查的是因式分解的应用.解决本题的关键是将m2+m作为一个整体出现,逐次降低m的次数.

练习册系列答案
相关题目
在①
;②
;③
;④
中,能与
合并的有( )
| 12 |
|
| 8 |
| 27 |
| 3 |
| A、①② | B、②③ |
| C、①②④ | D、①②③④ |
已知从一个多边形的一个顶点只可引出三条对角线,那么这个多边形是( )
| A、五边形 | B、六边形 |
| C、七边形 | D、八边形 |
计算(5
+
-6
)÷
的值为( )
| 48 |
| 12 |
| 27 |
| 3 |
| A、4 | B、-4 | C、2 | D、-2 |
 如图,是边长为1的正方形网格,则图中四边形的面积为( )
如图,是边长为1的正方形网格,则图中四边形的面积为( )| A、25 | B、12.5 |
| C、9 | D、8.5 |
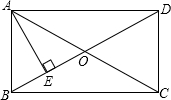 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE=
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作AE⊥BD,垂足为点E,若ED=3EO,AE= 某工厂要制作符合条件的模板,如图,要∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测∠BDC的度数的方法筛选出不合格的产品,若测∠BDC的度数为150°,则这种模板是否合格?请说明理由.
某工厂要制作符合条件的模板,如图,要∠A=105°,∠B=18°,∠C=30°,为了提高工作效率,检验人员利用测∠BDC的度数的方法筛选出不合格的产品,若测∠BDC的度数为150°,则这种模板是否合格?请说明理由.