题目内容
5.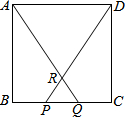 如图,正方形ABCD中,P,Q是BC边上的三等分点,连接AQ、DP交于点R.若正方形ABCD的面积为144cm2,则△PQR的面积为6cm2.
如图,正方形ABCD中,P,Q是BC边上的三等分点,连接AQ、DP交于点R.若正方形ABCD的面积为144cm2,则△PQR的面积为6cm2.
分析 根据BP=PQ=QC,由相似三角形的性质可得△PQR的底边=正方形ABCD边长的$\frac{1}{3}$,高是正方形ABCD边长的$\frac{1}{1+3}=\frac{1}{4}$,根据三角形的面积公式和已知条件即可求得△PQR的面积.
解答 解:∵四边形ABCD是正方形,
∴AD∥BC,
∴△PRQ∽△DRA,
∵BP=PQ=QC,
∴△PQR的底边=正方形ABCD边长的$\frac{1}{3}$,高是正方形ABCD边长的$\frac{1}{1+3}=\frac{1}{4}$,
∴△PQR的面积=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{4}$正方形ABCD的面积=$\frac{1}{24}$×144=6(cm2).
故答案为:6
点评 此题考查了正方形的性质,相似三角形的判定与性质,三角形的面积,关键是得到得△PQR的底边=正方形ABCD边长的$\frac{1}{3}$,高是正方形ABCD边长的$\frac{1}{4}$.

练习册系列答案
相关题目
10.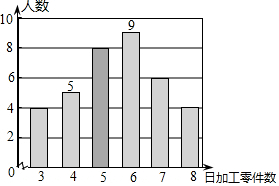 下面的条形图(如图)描述了某车间工人日加工零件的情况,则这些工人日加工零件数的中位数是( )
下面的条形图(如图)描述了某车间工人日加工零件的情况,则这些工人日加工零件数的中位数是( )
 下面的条形图(如图)描述了某车间工人日加工零件的情况,则这些工人日加工零件数的中位数是( )
下面的条形图(如图)描述了某车间工人日加工零件的情况,则这些工人日加工零件数的中位数是( )| A. | 6.5 | B. | 6 | C. | 5.5 | D. | 5 |
17.等腰三角形的一边长为4cm,另一条边长为8cm,则它的周长为( )
| A. | 16cm | B. | 20cm | C. | 12cm | D. | 16cm或20cm |
15.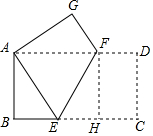 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |