题目内容
20. 如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A-B-C运动,设点P运动的时间为t秒.
如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A-B-C运动,设点P运动的时间为t秒.(1)当t为何值时,点P与点A的距离为5cm?
(2)当t为何值时,△APD是等腰三角形?
(3)当t为何值时,(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边?
分析 (1)分为两种情况:P在BC上,P在DC上,根据勾股定理得出关于t的方程,求出即可;
(2)分AD=DP,DP=AP,AD=AP三种情况进行讨论;
(3)求出BP=2t-4,CP=10-2t,根据AP2=AB2+BP2=42+(2t-4)2和AD2+CP2=AP2得出方程62+(10-2t)2=42+(2t-4)2,求出方程的解即可.
解答 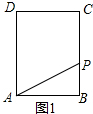 解:(1)如图1,若点P在BC上,
解:(1)如图1,若点P在BC上,
∵在Rt△ABP中,AP=5,AB=4
∴BP=2t-4=3,
∴t=$\frac{7}{2}$;
如图2,若点P在DC上,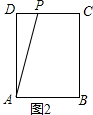
则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5.
综上所述,当t=$\frac{7}{2}$秒时,点P与点A的距离为5cm;
由于沿矩形的边A-B-C运动,此种情况不存在;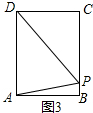
(2)当AD=DP时,如图3,PC=(10-2t)cm,CD=4cm,DP=6cm,
∵CD2+PC2=DP2,即42+(10-2t)2=62,解得t=5±$\sqrt{5}$,即t1=5+$\sqrt{5}$,t2=5-$\sqrt{5}$;
当DP=AP时,如图4,PC=PB=3cm,
∵AB=4cm,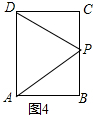
∴AB+BP=4+3=7cm,
∴t=$\frac{7}{2}$(秒);
当AD=AP=6时,PB=2t-4,
∵AB2+BP2=AP2,即42+(2t-4)2=62,解得t=2+$\sqrt{5}$或t=2-$\sqrt{5}$(舍去),
综上所述,当t=(5±$\sqrt{5}$)秒或t=$\frac{7}{2}$秒时,△APD是等腰三角形;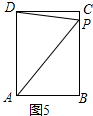
(3)当2<t<5时,点P在BC边上,
∵BP=2t-4,CP=10-2t,
∴AP2=AB2+BP2=42+(2t-4)2
由题意,有AD2+CP2=AP2
∴62+(10-2t)2=42+(2t-4)2
∴t=$\frac{13}{3}$<5,
∴t=$\frac{13}{3}$.
答:当t=$\frac{13}{3}$秒时,以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.
点评 本题考查的是四边形综合题,涉及到等腰三角形的判定与性质、勾股定理、直角三角形的性质等知识,解答此题时要注意进行分类讨论.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案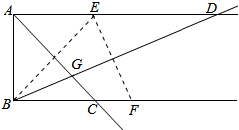 如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )
如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )| A. | tan∠ADB=$\sqrt{2}$-1 | B. | ∠DEF=67.5° | C. | ∠AGB=∠BEF | D. | cos∠AGB=$\frac{\sqrt{6}}{4}$ |
 如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )
如图,根据a、b、c三个数表示在数轴上的情况,下列关系正确的是( )| A. | a<c | B. | a+b<0 | C. | |a|<|c| | D. | bc<0 |
 已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F,
已知:如图:AB∥CD,AB=CD,AD、BC相交于点O,BE∥CF,BE、CF分别交AD于点E、F, 如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角. 如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.
如图,在△ABC中,AB=AC=10m,BC=16m,现点P从点B出发,沿BC向C点运动,运动速度为$\frac{1}{4}$m/s,若点P的运动时间为t秒,则当△ABP是直角三角形时,时间t的值为32s或50s.