题目内容
13.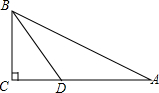 已知,如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=$\frac{1}{2}$AB,BD=4,则点D到AB的距离为( )
已知,如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=$\frac{1}{2}$AB,BD=4,则点D到AB的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法确定 |
分析 由∠C=90°,BC=$\frac{1}{2}$AB,得到∠A=30°,根据三角形的内角和得到∠ABC=60°,根据角平分线的性质得到∠CBD=$\frac{1}{2}∠$ABC=30°,由直角三角形的性质得到CD=$\frac{1}{2}$BD=2,过D作DE⊥AB于E,然后根据角平分线的性质即可得到结论.
解答  解:∵∠C=90°,BC=$\frac{1}{2}$AB,
解:∵∠C=90°,BC=$\frac{1}{2}$AB,
∴∠A=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠CBD=$\frac{1}{2}∠$ABC=30°,
∴CD=$\frac{1}{2}$BD=2,
过D作DE⊥AB于E,
∴DE=CD=2,
∴点D到AB的距离为2,故选A.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,含30°角的直角三角形的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
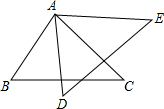 已知△ABC≌△ADE,如果∠BAE=135°,∠BAD=40°,那么∠BAC=95°.
已知△ABC≌△ADE,如果∠BAE=135°,∠BAD=40°,那么∠BAC=95°. 已知关于x、y的方程组$\left\{\begin{array}{l}{ax-3y=5}\\{6x+by=-2}\end{array}\right.$所对应的两个一次函数的图象如图所示,求a-b的值.
已知关于x、y的方程组$\left\{\begin{array}{l}{ax-3y=5}\\{6x+by=-2}\end{array}\right.$所对应的两个一次函数的图象如图所示,求a-b的值.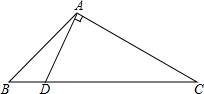 已知:如图,在△ABC中,∠B=2∠C,DA⊥AC交BC于D,求证:CD=2AB.
已知:如图,在△ABC中,∠B=2∠C,DA⊥AC交BC于D,求证:CD=2AB.
 如图,BC是⊙O的弦,OA⊥BC,垂足为A,若⊙O的半径为13,BC=24,则线段OA的长为( )
如图,BC是⊙O的弦,OA⊥BC,垂足为A,若⊙O的半径为13,BC=24,则线段OA的长为( )