题目内容
3. 如图,BC是⊙O的弦,OA⊥BC,垂足为A,若⊙O的半径为13,BC=24,则线段OA的长为( )
如图,BC是⊙O的弦,OA⊥BC,垂足为A,若⊙O的半径为13,BC=24,则线段OA的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由垂径定理得出AB=$\frac{1}{2}$BC=12,∠OAB=90°,由勾股定理求出OA即可.
解答 解:连接OB,如图所示:
∵OA⊥BC,
∴AB=$\frac{1}{2}$BC=12,∠OAB=90°,
由勾股定理得:OA=$\sqrt{O{B}^{2}-A{B}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5;
故选:A.
点评 本题考查了垂径定理、勾股定理;熟练掌握垂径定理,运用勾股定理求出OA是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
14.下列条件能说明OC是∠AOB平分线的是( )
| A. | ∠AOC=$\frac{1}{2}$∠AOB | B. | ∠BOC=$\frac{1}{2}$∠AOB | C. | ∠AOC=2∠AOB | D. | ∠AOC=∠AOB |
18.拒绝“餐桌浪费”刻不容缓,据统计全国每年浪费食物总量约为50 000 000 000千克,将50 000 000 000用科学记数法表示为( )
| A. | 0.5×1011 | B. | 5×1010 | C. | 5×109 | D. | 50×109 |
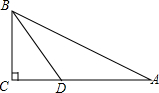 已知,如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=$\frac{1}{2}$AB,BD=4,则点D到AB的距离为( )
已知,如图,在△ABC中,∠C=90°,BD平分∠ABC,BC=$\frac{1}{2}$AB,BD=4,则点D到AB的距离为( ) 如图,已知a∥b,∠1=55°,则∠2=125°.
如图,已知a∥b,∠1=55°,则∠2=125°.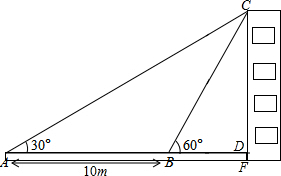 如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).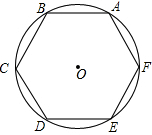 已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正方形的周长和面积.
已知正六边形ABCDEF,如图所示,其外接圆的半径是a,求正方形的周长和面积.