题目内容
3．
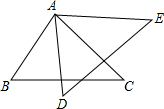已知△ABC≌△ADE，如果∠BAE=135°，∠BAD=40°，那么∠BAC=95°．
分析 求出∠DAE=95°，根据全等三角形的性质求出∠BAC=∠DAE，代入求出即可．
解答 解：∵∠BAE=135°，∠BAD=40°，
∴∠∠DAE=∠BAE-∠BAD=95°，
∵△ABC≌△ADE，
∴∠BAC=∠DAE=95°，
故答案为：95°．
点评 本题考查了全等三角形的性质的应用，能根据全等三角形的性质求出∠BAC=∠DAE是解此题的关键，注意：全等三角形的对应角相等，对应边相等．
练习册系列答案
一本好题口算题卡系列答案
相关题目
13．下列各数中，既不是正数也不是负数的是（ ）
| A． | 0 | B． | -2 | C． | 1 | D． | $\frac{1}{2}$ |
14．一位病人每天下午需要测量一次血压，下表是该病人本周星期一至星期五收缩压的变化情况．（“+”表示上升，“-”表示下降）
（1）本周三与周一相比收缩压下降（填“上升”或“下降”）；
（2）通过计算说明本周五收缩压与上周日相比是上升了还是下降了，并求出上升或下降了多少；
（3）如果该病人本周五的收缩压为185，那么他上个周日的收缩压为多少？
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 收缩压的变化 （与前一天比较） | +30 | -20 | +17 | +18 | -20 |
（2）通过计算说明本周五收缩压与上周日相比是上升了还是下降了，并求出上升或下降了多少；
（3）如果该病人本周五的收缩压为185，那么他上个周日的收缩压为多少？
18．下列分式中，一定有意义的是（ ）
| A． | $\frac{x-3}{{x}^{2}-4}$ | B． | $\frac{y-1}{{y}^{2}+1}$ | C． | $\frac{{x}^{2}+1}{3x}$ | D． | $\frac{x-1}{x+1}$ |
8．
如图，点B，O，D在同一条直线上，∠1=15°，∠AOC=90°，则∠2的度数为（ ）
如图，点B，O，D在同一条直线上，∠1=15°，∠AOC=90°，则∠2的度数为（ ）| A． | 15° | B． | 75° | C． | 105° | D． | 165° |
15．已知点P（m，2）与Q（3，n）关于y轴对称，则（m+n）2015的值为（ ）
| A． | -1 | B． | 1 | C． | 52015 | D． | -52015 |
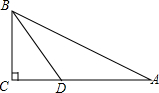已知，如图，在△ABC中，∠C=90°，BD平分∠ABC，BC=$\frac{1}{2}$AB，BD=4，则点D到AB的距离为（ ）