题目内容
8．
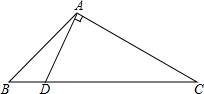已知：如图，在△ABC中，∠B=2∠C，DA⊥AC交BC于D，求证：CD=2AB．
分析 取CD的中点E，连接AE，根据直角三角形斜边上的中线等于斜边的一半可得AE=CE=$\frac{1}{2}$CD，根据等边对等角可得∠C=∠CAE，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEB=2∠C=∠B，根据等角对等边可得AE=AB，即可得证．
解答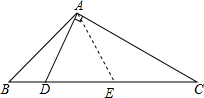 
证明：如图，取CD的中点E，连接AE，
∵AD⊥AC，
∴AE=CE=$\frac{1}{2}$CD，
∴∠C=∠CAE，
∴∠AEB=∠C+∠CAE=2∠C，
∵∠B=2∠C，
∴∠AEB=∠B，
∴AE=AB，
∴AB=$\frac{1}{2}$CD，
∴CD=2AB．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的判定与性质，作辅助线利用性质并构造出等腰三角形是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
18．下列分式中，一定有意义的是（ ）
| A． | $\frac{x-3}{{x}^{2}-4}$ | B． | $\frac{y-1}{{y}^{2}+1}$ | C． | $\frac{{x}^{2}+1}{3x}$ | D． | $\frac{x-1}{x+1}$ |
3．判断下列变量之间的关系是不是函数关系，是的画“√”，不是的画“×”，并在横线上写出理由．
（1）高线长h的等腰三角形的底边长a与面积S．（ ）√；
（2）关系式y=±$\sqrt{x}$中的y与x．（ ）×．
（3）下表中的v与s．（ ）√．
（4）关系式y=x2中的y与x．（ ）×．
（1）高线长h的等腰三角形的底边长a与面积S．（ ）√；
（2）关系式y=±$\sqrt{x}$中的y与x．（ ）×．
（3）下表中的v与s．（ ）√．
| 助跑速度v（m/s） | 7.5 | 8 | 8.5 |
| 跳远的距离s（m） | 4.78 | 5.44 | 6.14 |
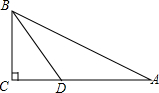已知，如图，在△ABC中，∠C=90°，BD平分∠ABC，BC=$\frac{1}{2}$AB，BD=4，则点D到AB的距离为（ ）
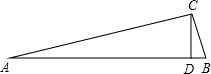已知：如图，在Rt△ABC中，∠C=90°，∠B=5∠A，CD⊥AB，垂足为D，求证：AB=4CD．（提示．作斜边AB上的中线CM）
18．拒绝“餐桌浪费”刻不容缓，据统计全国每年浪费食物总量约为50 000 000 000千克，将50 000 000 000用科学记数法表示为（ ）
| A． | 0.5×1011 | B． | 5×1010 | C． | 5×109 | D． | 50×109 |