题目内容
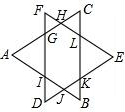 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.(1)求证:△FGH和△CHL和△LEK和△KBJ和△JDI和△IAG都是等边三角形.(或证明∠AGF=∠FHC=∠CLE=∠EKB=∠BJI=∠DIA=120°)
(2)求等边△ABC的边长.
考点:等边三角形的判定与性质
专题:
分析:(1)由图中位置和已知条件容易得出:∠F=60°,FG=FH,FD=BC,因此△FGH是等边三角形;
(2)利用等边三角形的性质推知重叠部分的周长为FD+BC=6,易求FD=BC=3.
(2)利用等边三角形的性质推知重叠部分的周长为FD+BC=6,易求FD=BC=3.
解答: 解:(1)∵△ABC和△DEF都是等边三角形,
解:(1)∵△ABC和△DEF都是等边三角形,
∴∠F=60°,FG=FH,FD=BC,
∴△FGH是等边三角形,
同理△CHL、△LEK、△KBJ、△JDI、△TAG都是等边三角形;
(2)∵△FGH是等边三角形,
∴GH=FG.
同理,IJ=ID,HL=CL,JK=KB,
∴重叠部分的周长为:FD+BC=6,
∴FD=BC=3,
即等边△ABC的边长是 3.
 解:(1)∵△ABC和△DEF都是等边三角形,
解:(1)∵△ABC和△DEF都是等边三角形,∴∠F=60°,FG=FH,FD=BC,
∴△FGH是等边三角形,
同理△CHL、△LEK、△KBJ、△JDI、△TAG都是等边三角形;
(2)∵△FGH是等边三角形,
∴GH=FG.
同理,IJ=ID,HL=CL,JK=KB,
∴重叠部分的周长为:FD+BC=6,
∴FD=BC=3,
即等边△ABC的边长是 3.
点评:本题考查了等边三角形的判定与性质,根据题意推知△FGH是等边三角形是解题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一副直角三角板按如图所示的方式摆放,其中点C在FD的延长线上,且AB∥FC,则∠CBD的度数为( )
一副直角三角板按如图所示的方式摆放,其中点C在FD的延长线上,且AB∥FC,则∠CBD的度数为( )| A、15° | B、20° |
| C、25° | D、30° |
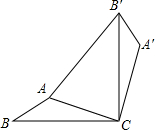 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )| A、125° | B、130° |
| C、135° | D、140° |
 现将连续自然数1至2007在图中的方式排成一个长方形阵列,用一个矩形框出16个数
现将连续自然数1至2007在图中的方式排成一个长方形阵列,用一个矩形框出16个数 如图,已知AB、AC为⊙O的两条弦,D、E分别是
如图,已知AB、AC为⊙O的两条弦,D、E分别是
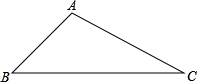 如图,在△ABC中,∠B=45°,∠C=15°,BC=5
如图,在△ABC中,∠B=45°,∠C=15°,BC=5 已知CA、BE分别垂直AB于A点和B点,∠CDE=90°,
已知CA、BE分别垂直AB于A点和B点,∠CDE=90°,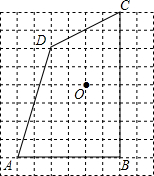 如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点.
如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点. 如图,矩形ABCD的面积为1,它的两条对角线交于点O1,取BO1的中点O2,连AO2并延长到C1,使得AO2=C1O2,得到四边形ABC1O1,同样取BO2的中点O3,连AO3并延长到C2,使得AO3=C2O3,得到四边形ABC2O2…依此类推,可作得四边形ABCnOn.
如图,矩形ABCD的面积为1,它的两条对角线交于点O1,取BO1的中点O2,连AO2并延长到C1,使得AO2=C1O2,得到四边形ABC1O1,同样取BO2的中点O3,连AO3并延长到C2,使得AO3=C2O3,得到四边形ABC2O2…依此类推,可作得四边形ABCnOn.