题目内容
如图所示，O是直线AB上一点，∠AOC：∠BOC=1：2，∠COD：∠AOC=1：2．（1）求∠COD的度数；
（2）判断OD与AB的位置关系，并说明理由．
考点：垂线
专题：
分析：（1）设未知数∠COD=x，得∠AOC=2x，∠BOC=4x，根据题意列出方程，解方程即可求出∠COD=30°；
（2）根据（1）的结果得出∠AOC=60°，求出∠AOD=90°，证出OD⊥AB．
（2）根据（1）的结果得出∠AOC=60°，求出∠AOD=90°，证出OD⊥AB．
解答：解：（1）设∠COD=x，则∠AOC=2x，∠BOC=4x；
根据题意得：2x+4x=180°，
解得：x=30°，
即∠COD=30°；
（2）OD⊥AB；理由如下：
由（1）得∠AOC=60°，
∴∠AOD=60°+30°=90°，
∴OD⊥AB．
根据题意得：2x+4x=180°，
解得：x=30°，
即∠COD=30°；
（2）OD⊥AB；理由如下：
由（1）得∠AOC=60°，
∴∠AOD=60°+30°=90°，
∴OD⊥AB．
点评：本题考查了垂线的定义；弄清各个角之间的数量关系，列出方程是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知AB、AC为⊙O的两条弦，D、E分别是
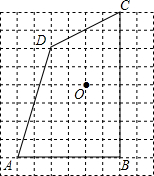如图，在9×9网络图中，每个正方形边长均为1，点O和四边形ABCD的顶点均为小正方形的顶点．
如图，Rt△ABC中，∠BAC=90°，∠ACB=30°，点A的坐标为（3，0），过点B的双曲线y=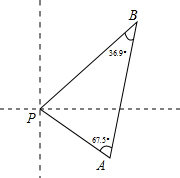
我南海巡逻船接到有人落水求救信号，如图，巡逻船A观测到∠PAB=67.5°，同时，巡逻船B观测到∠PBA=36.9°，两巡逻船相距63海里，求此时巡逻船A与落水人P的距离？（参考数据：sin36.9°≈
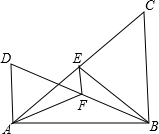如图，∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点．
如图，矩形ABCD的面积为1，它的两条对角线交于点O1，取BO1的中点O2，连AO2并延长到C1，使得AO2=C1O2，得到四边形ABC1O1，同样取BO2的中点O3，连AO3并延长到C2，使得AO3=C2O3，得到四边形ABC2O2…依此类推，可作得四边形ABCnOn．