题目内容
将二次函数y=2(x+1)2+4图象向右平移2个单位,再向下平移1个单位所得图象函数解析式为 .
考点:二次函数图象与几何变换
专题:
分析:先得到y=2(x+1)2+4的顶点坐标为(-1,4),然后把点(-1,4)向右平移2个单位,再向下平移1个单位得到(1,3);再根据抛物线的顶点式:y=a(x-h)2+k(a≠0)直接写出解析式.
解答:解:∵y=2(x+1)2+4的顶点坐标为(-1,4),
∴把点(-1,4)向右平移2个单位,再向下平移1个单位得到(1,3)
而平移的过程中,抛物线的形状没改变,
∴所得的新抛物线的解析式为:y=2(x-1)2+3.
故答案是:y=2(x-1)2+3.
∴把点(-1,4)向右平移2个单位,再向下平移1个单位得到(1,3)
而平移的过程中,抛物线的形状没改变,
∴所得的新抛物线的解析式为:y=2(x-1)2+3.
故答案是:y=2(x-1)2+3.
点评:本题考查了抛物线的几何变换:抛物线的平移问题可转化为其顶点的平移问题,抛物线的顶点式:y=a(x-h)2+k(a≠0),则抛物线的顶点坐标为(h,k).

练习册系列答案
相关题目
化简:(1+
)÷
的结果为( )
| 1 |
| x |
| x2-1 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
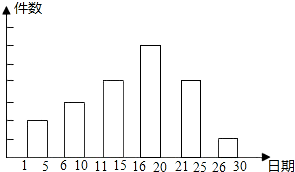 学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.
学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12. 如图是二次函数y=ax2+bx+a2-2(a、b为常数)的图象,则a=
如图是二次函数y=ax2+bx+a2-2(a、b为常数)的图象,则a= 如图,已知BO是△ABC的外接圆的半径,CD⊥AB于D.若AD=3,BD=8,CD=6,则BO的长为
如图,已知BO是△ABC的外接圆的半径,CD⊥AB于D.若AD=3,BD=8,CD=6,则BO的长为 如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.
如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.