题目内容
如图，在?ABCD中，点E、F分别在边BC和AD上，且BE=DF．（1）求证：△ABE≌△CDF；
（2）求证：AE=CF．
考点：平行四边形的性质,全等三角形的判定与性质
专题：几何综合题
分析：（1）根据平行四边形的性质得出AB=CD，∠B=∠D，根据SAS证出△ABE≌△CDF；
（2）根据全等三角形的对应边相等即可证得．
（2）根据全等三角形的对应边相等即可证得．
解答：证明：∵四边形ABCD是平行四边形，
∴AB=CD，∠B=∠D，
在△ABE和△CDF中，
∴△ABE≌△CDF（SAS），
∴AE=CF．
∴AB=CD，∠B=∠D，
在△ABE和△CDF中，
|
∴△ABE≌△CDF（SAS），
∴AE=CF．
点评：本题主要考查对平行四边形的性质，全等三角形的性质和判定等知识点的理解和掌握，能根据性质证出△ABE≌△CDF是证此题的关键．
练习册系列答案
相关题目
如图的几何体的左视图是（ ）
A、 |
B、 |
C、 |
D、 |
如图，△ABC的三个顶点位置分别是A（1，0），B（-3，0），C（-2，5）．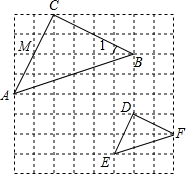
如图，在8×8的正方形网格中，△CAB和△DEF的顶点都在边长为1的小正方形的顶点上，AC与网格上的直线相交于点M．
如图，∠1=∠2，则∠1与∠3的数量关系时