题目内容
19．
如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOE=140°，∠COD=30°，求∠AOB的度数．
分析 根据角平分线的定义可求出∠BOC=∠AOB，∠COD=∠DOE，从而可求出∠AOB的度数．
解答 解：∵OB是∠AOC的平分线，OD是∠COE的平分线，
∴∠COB+∠DOC=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×140°=70°
又∵∠COD=30°
∴∠AOB=∠BOC=40°．
点评 本题考查角平分线的定义，解题的关键是求出∠BOC=∠AOB，∠COD=∠DOE，本题属于基础题型．
练习册系列答案
相关题目
4．下列等式从左到右的变形，属于因式分解的是（ ）
| A． | m（a+b）=ma+mb | B． | X2+2x+1=x（x+2）+1 | C． | （x+1）（x-1）=x2-1 | D． | x3-x=x（x+1）（x-1） |
（1）解方程：$\frac{x}{x-2}$=$\frac{2}{x-2}$-1
8．
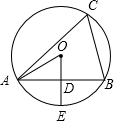如图⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，若⊙O的半径为2，则下列结论错误的是（ ）
如图⊙O是△ABC的外接圆，OD⊥AB于点D，交⊙O于点E，∠C=60°，若⊙O的半径为2，则下列结论错误的是（ ）| A． | AD=BD | B． | AE=BE | C． | AB=$\sqrt{3}$ | D． | OD=1 |