题目内容
16. 如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )
如图,沿AC方向开山修路,为加快施工进度,要在小山的另一边同时施工.现在AC上取一点B,使∠ABD=145°,BD=500 m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离为( )| A. | 500•sin55° m | B. | 500•cos55° m | C. | 500•tan55° m | D. | $\frac{50}{cos55°}{m}$ |
分析 根据题意和锐角三角函数可以得到DE的长与BD的关系,从而可以解答本题.
解答 解:由题意可得,
∠DBC=180°-∠ABD=180°-145°=35°,BD=500m,
∴要使A,C,E成一直线,则∠DEB=180°-∠DBE-∠D=90°,
∴DE=BD•cos50°=500•cos55°,
故选B.
点评 本题考查解直角三角形的应用,解答此类问题的关键是明确题意,利用锐角三角函数解答.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
4.下列等式从左到右的变形,属于因式分解的是( )
| A. | m(a+b)=ma+mb | B. | X2+2x+1=x(x+2)+1 | C. | (x+1)(x-1)=x2-1 | D. | x3-x=x(x+1)(x-1) |
8.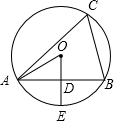 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
 如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )
如图⊙O是△ABC的外接圆,OD⊥AB于点D,交⊙O于点E,∠C=60°,若⊙O的半径为2,则下列结论错误的是( )| A. | AD=BD | B. | AE=BE | C. | AB=$\sqrt{3}$ | D. | OD=1 |
 (1)解方程:$\frac{x}{x-2}$=$\frac{2}{x-2}$-1
(1)解方程:$\frac{x}{x-2}$=$\frac{2}{x-2}$-1