题目内容
1.关于x的不等式组$\left\{\begin{array}{l}{x-1≥0}\\{a-x≥0}\end{array}\right.$有四个整数解,则a的取值范围是4≤a<5.分析 将不等式x-1≥0的解集表示在数轴上,并在其范围内确定四个最小的整数,然后再分析x≤a使得两个不等式组的解集的公共部分中正好有这四个整数即可.
解答 解:$\left\{\begin{array}{l}{x-1≥0}&{①}\\{a-x≥0}&{②}\end{array}\right.$
解①得:x≥1,
解②得:x≤a,
因为原不等式组有四个整数解,如下图所示: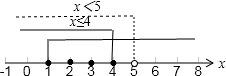
由上图可知当x<5或x≤4都能使原不等式组有四个整数解,
所以,a的取值范围是:4≤a<5
点评 本题考查了一元一次不等式组中待定字母的取值范围,关键是要使得$\left\{\begin{array}{l}{x≥1}\\{x≤a}\end{array}\right.$中有四个整数解,要注意a的取值是一个区间.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
12.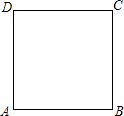 如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
 如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )
如图,正方形ABCD的边长为4,一动点P从A出发,沿正方形的边逆时针运动,运动的方式为:每前进5个单位,后退3个单位.已知P点每秒前进或后退1个单位,xn表示第n秒P点与A点的距离,则x2015等于( )| A. | $\sqrt{17}$ | B. | 3 | C. | 5 | D. | 2$\sqrt{5}$ |
9.数据x1,x2,…,xn的极差为0,则这组数据的方差为( )
| A. | 1 | B. | 0 | C. | n2 | D. | 不能确定 |

 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.点O是AC的中点,过点O的直线l与AB边相交于点D.过点C作CE∥AB交直线l于点E,设∠AOD=α.解答下列问题:
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.点O是AC的中点,过点O的直线l与AB边相交于点D.过点C作CE∥AB交直线l于点E,设∠AOD=α.解答下列问题: 如图,AB∥CD,EB∥DF,试说明∠1=∠2.
如图,AB∥CD,EB∥DF,试说明∠1=∠2.