题目内容
8.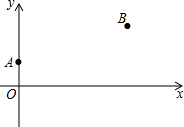 如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.
如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.
分析 作A关于x轴的对称点A′,则A′坐标为(0,-1),连接A′B,与x轴的交点即P点.然后根据A′、B的坐标通过待定系数法求得直线A′B的解析式,即可求得P的坐标.作BC⊥y轴于C,在Rt△A′BC中,根据勾股定理即可求得水管最短的长度.
解答 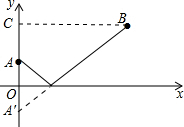 解:作A关于x轴的对称点A′,则A′坐标为(0,-1).
解:作A关于x轴的对称点A′,则A′坐标为(0,-1).
连接A′B,与x轴的交点即P点.
∵PA=PA′,
∴AP+PB=A′P+PB=A′B(水管最短).
因为A′(0,-1),B(4,2),
设直线A′B的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=-1}\\{4k+b=2}\end{array}\right.$,交点$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-1}\end{array}\right.$
∴直线A′B的解析式为y=$\frac{3}{4}$x-1,
令y=0,则0=$\frac{3}{4}$x-1,解得x=$\frac{4}{3}$,
∴P点坐标为($\frac{4}{3}$,0).
作BC⊥y轴于C,
在Rt△A′BC中,A′C=3,BC=4,
所以A′B=$\sqrt{A{′C}^{2}+B{C}^{2}}$=5.
即水管最短的长度为5km.
点评 本题考查了在平面直角坐标系中确定点的坐标,在平面直角坐标系中用轴对称和勾股定理求最短距离,待定系数法求一次函数解析式.此类题型是个重点也是难点,需要掌握.

练习册系列答案
相关题目
19.下列计算中,正确的是( )
| A. | (a+b)2=a2+b2 | B. | (2a-b)2=4a2-b2 | C. | (x+3)(x-2)=x2-6 | D. | (x+3)(x-3)=x2-9 |
13.计算(a-1)2,正确的结果是( )
| A. | a-2 | B. | a2 | C. | a-1 | D. | a |
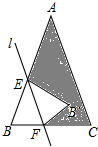 等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断:
等腰三角形ABC中,顶角A是大于0°小于180°的任意角,直接l∥AC并AB于E,交BC于F,沿直线l折叠角B,点B的对应点为B′,请对以下结论做出判断: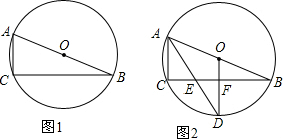
 如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.
如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.