题目内容
如图，AB∥FC，DE＝EF，AB＝15，CF＝8，则BD等于( )
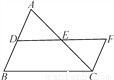
A. 8 B. 7 C. 6 D. 5
B
【解析】∵AB//CF，
∴∠A=∠ECF，
又∵DE=EF，∠AED=∠CEF，
∴△ADE≌△CFE，
∴AD=CF=8，
∴BD=AB-AD=15-8=7，
故选B.
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
如图，点E在BC的延长线上，下列条件中能判定BC//AD的是 ( )
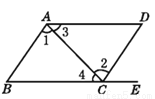
A. ∠1=∠2 B. ∠DAB+∠D=180° C. ∠3=∠4 D. ∠B=∠DCE
C
【解析】A. ∵∠1=∠2 ，∴AB∥CD, 故不正确；
B. ∵ ∠DAB+∠D=180° ，∴AB∥CD, 故不正确；
C. ∵∠3=∠4 ，∴ BC∥AD, 故正确；
D. ∵∠B=∠DCE，∴AB∥CD, 故不正确；
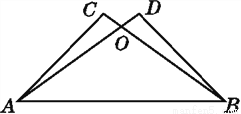
故选C. 如图,△ACB与△BDA全等,AC与BD对应,BC与AD对应,写出其余的对应边和对应角.
见解析
【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系．
试题解析: ∵ △ACB≌△BDA,
∴AB=BA;∠CBA=∠DAB,∠CAB=∠DBA,∠C=∠D. （10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD
可证明△EBM≌△FCM，
得∠EMB≌△FCM，
得∠EMB＝∠FMC，
∵∠CMF＋∠BMF＝180°
∴∠BME＋∠BMF＝180°
∴E、F、M恰好在一直线上
【解析】分析：三角形全等条件中必须是三个元素，本题已经有两条对应边相等，只要再找到它们的夹角相等就可以了．
解答：证明：∵BE、CF分别是AC、AB两条边上的高，
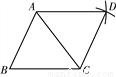
∴∠ABD+∠BAC... 如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为______度.
65
【解析】试题分析：∵以点A为圆心，以BC长为半径作弧；以顶点C为圆心，以AB长为半径作弧，两弧交于点D，
∴AB=CD，BC=AD，
在△ABC和△CDA中，
∵AB=CD，BC=AD，AC=CA，
∴△ABC≌△CDA（SSS），
∴∠ADC=∠B=65°．
故答案是65°． 已知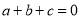
， 
.
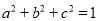（1）求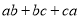
的值；
（2）求
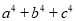的值．
（1） （2）
【解析】试题分析：（1）把a+b+c=0两边平方，然后利用代入法等量代换即可；
（2）把ab+bc+ca与两边分别乘方即可.
试题解析：（1）因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
（2）因为a+b+c=0，a2+b2+c2=1
所以+2ab+2ac+2bc=0
... 某班黑板是一个长方形，它的面积为6a2－9ab＋3a，已知这个长方形的长为3a，则宽为_____.
2a-3b+1
【解析】由题意可得，长方形的宽为：（6a2－9ab＋3a）÷3a=2a-3b+1. 在长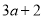为
，宽为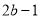
的长方形铁片上，挖去长为
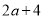，宽为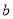
的小长方形铁片，求剩余部分面积。
4ab-3a-2
【解析】试题分析：根据长方形的面积=长×宽，利用大长方形的面积减去小长方形的面积即可.
试题解析：（3a+2）（2b-1）-（2a+4）b
=6ab+4b-3a-2-2ab-4b
=4ab-3a-2 用“●”“■”“”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（ ）
A．2个 B．3个 C．4个 D．5个
D
【解析】
试题分析：设“●”“■”“”分别为x、y、z，由图可知，
，解得x=2y，z=3y，
所以x+z=2y+3y=5y，即“■”的个数为5，
故选D．