题目内容
5．若关于x的分式方程$\frac{2x-a}{x-1}$=1的解为正数，则字母a的取值范围是（ ）| A． | a＜2 | B． | a≠2 | C． | a＞1 | D． | a＞1且a≠2 |
分析 首先解关于x的方程，利用a表示出x的值，然后根据分母不等于0，且解是正数求得a的范围．
解答 解：去分母，得2x-a=x-1，
解得x=a-1，
则a-1＞0且a-1-1≠0，
解得a＞1且a≠2．
故选D．
点评 本题考查了分式方程的解，正确解关于x的方程，以及注意到x-1≠0是关键．
练习册系列答案
相关题目
15．长方形的一边长为3x+2y，另一边长为2x-3y，则这个长方形的周长是（ ）
| A． | 10x-2y | B． | 4x+y | C． | x-4y | D． | 5x-y |
16．用12m长的铝材制成一个矩形窗框，使它的面积为8m2，若设它的一条边长为xm，则根据题意可列出关于x的方程为（ ）
| A． | x（6-x）=8 | B． | x（6+x）=8 | C． | x（12-x）=8 | D． | x（12-2x）=8 |
13．
如图，已知△ABC的高AD，角平分线AE，∠B=24°，∠ACD=56°，那么∠AED的度数是（ ）
如图，已知△ABC的高AD，角平分线AE，∠B=24°，∠ACD=56°，那么∠AED的度数是（ ）| A． | 45° | B． | 42° | C． | 41° | D． | 40° |
20．如果将抛物线y=x2+3向下平移1个单位，那么所得新抛物线的解析式是（ ）
| A． | y=（x-1）2+3 | B． | y=（x+1）2+3 | C． | y=x2+2 | D． | y=x2+4 |
10．若式子m$\sqrt{-\frac{1}{m}}$有意义，则化简此式等于（ ）
| A． | $\sqrt{m}$ | B． | $\sqrt{-m}$ | C． | -$\sqrt{m}$ | D． | -$\sqrt{-m}$ |
5．一个圆柱的底面半径为Rcm，高为8cm，若它的高不变，将底面半径增加了2cm，体积相应增加了192πcm，则R=（ ）
| A． | 4cm | B． | 5cm | C． | 6cm | D． | 7cm |
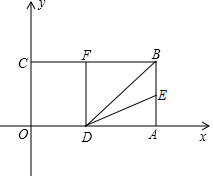如图，以长方形OABC的顶点O为原点，OA所在直线为x轴，OC所在直线为y轴，建立平面直角坐标系．已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，连结BD，点A关于BD的对称点恰好落在线段BC边上的点F处．