题目内容
20．如果将抛物线y=x2+3向下平移1个单位，那么所得新抛物线的解析式是（ ）| A． | y=（x-1）2+3 | B． | y=（x+1）2+3 | C． | y=x2+2 | D． | y=x2+4 |
分析 先确定抛物线y=x2+3的顶点坐标为（0，3），再利用点平移的规律得到点（0，3）平移后所得对应点的坐标为（0，2），然后根据顶点式写出新抛物线的解析式．
解答 解：抛物线y=x2+3的顶点坐标为（0，3），点（0，3）向下平移1个单位所得对应点的坐标为（0，2），所以新抛物线的解析式为y=x2+2．
故选C．
点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
10．抛物线y=x2-bx+9的顶点在坐标轴上，则b的值为（ ）
| A． | 6 | B． | ±6 | C． | ±6或0 | D． | 0 |
11．多项式12ab3c+8a3b的各项公因式是（ ）
| A． | 4ab2 | B． | 4abc | C． | 2ab2 | D． | 4ab |
8．下列方程中，解为x=4的方程是（ ）
| A． | x-2=6 | B． | $\frac{1}{3}$x=12 | C． | 2x+2=6 | D． | $\frac{1}{2}$（x-2）=1 |
15．一种细菌的半径约为0.00004米，这个数用科学记数法表示为（ ）
| A． | 4×10-5 | B． | 0.4×10-6 | C． | 4×10-4 | D． | 40×10-4 |
5．若关于x的分式方程$\frac{2x-a}{x-1}$=1的解为正数，则字母a的取值范围是（ ）
| A． | a＜2 | B． | a≠2 | C． | a＞1 | D． | a＞1且a≠2 |
如图，Rt△ABC中，∠A=90°，D是BC的中点，E、F分别是AB、AC上的点，DE⊥DF．求证：EF2=BE2+CF2．（提示：要延长ED或FD，还要连接几条线段）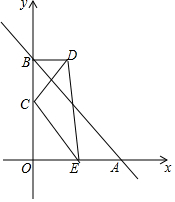
如图，在平面直角坐标系中，直线AB与x轴交于点A（4，0），与y轴交于点B（0，4），点E（2，0）在OA上，点C的坐标为（0，m）（m≠4），点C关于AB的对称点是点D，连结BD，CD，CE，DE