题目内容
6.对x、y定义一种新运算“P”,规定:P(x,y)=$\frac{ax+by}{3x+y}$(其中a、b均为非零常数),这里等号右边是通常的四则运算.例如:P(0,1)=$\frac{a×0+b×1}{3×0+1}$=b.(1)已知P(1,-1)=-2,P(4,2)=1.
①求a、b的值;
②关于m的不等式P(3m,14-9m)≥2的非负整数解;
(2)若P(x,y)=P(y,x)对任意x、y都成立(这里的P(x,y)和P(y,x)均有意义),则a、b之间应满足怎样的关系式?
分析 (1)①根据新定义得$\frac{a-b}{3-1}$=-2,$\frac{4a+2b}{12+2}$=1,然后解关于a、b的方程组即可;
②根据新定义得$\frac{3m+5(14-9m)}{9m+14-9m}$≥2,然后解关于m的一元一次不等式,再在解集内找出非负整数即可;
(2)根据新定义得$\frac{ax+by}{3x+y}$=$\frac{ay+bx}{3y+x}$,然后利用分式的性质变形后,因式分解得到(a-3b)(x2-y2)=0,再利用两有理数相乘的性质可得到a与b的关系.
解答 解:(1)①P(1,-1)=$\frac{a-b}{3-1}$=-2,P(4,2)=$\frac{4a+2b}{12+2}$=1,
即$\left\{\begin{array}{l}{a-b=-4}\\{4a+2b=14}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=5}\end{array}\right.$;
②根据题意得$\frac{3m+5(14-9m)}{9m+14-9m}$≥2,
即3m+5(14-9m)≥28,
去括号、移项得3m-45m≥28-70,
合并得-42m≥-42
系数化为1得m≤1,
所以不等式的非负整数解为0,1;
(2)根据题意得$\frac{ax+by}{3x+y}$=$\frac{ay+bx}{3y+x}$,
整理得(a-3b)(x2-y2)=0,
因为对任意x、y都成立,
所以a-3b=0,即a=3b.
点评 本题考查了一元一次不等式的整数解:解决此类问题的关键在于正确解得不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式的整数解.可以借助数轴进行数形结合,得到需要的值,进而非常容易的解决问题.解决本题的关键是对新定义的理解.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案①不等式有无数个解;②-x<-4;③1010是不等式的解;④x可以取4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
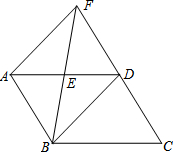 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.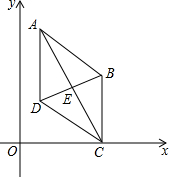 如图,在平面直角坐标系中,点A(1,4)B(m,n)(m>2),D(1,q)(q<n),点B、D在直线y=$\frac{1}{2}$x+1上,四边形ABCD的对角线AC,BD相交于点E.且AB∥CD,点C在x轴上,BE=DE.求证:四边形ABCD是菱形.
如图,在平面直角坐标系中,点A(1,4)B(m,n)(m>2),D(1,q)(q<n),点B、D在直线y=$\frac{1}{2}$x+1上,四边形ABCD的对角线AC,BD相交于点E.且AB∥CD,点C在x轴上,BE=DE.求证:四边形ABCD是菱形.
