题目内容
15.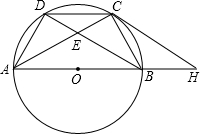 如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.
如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.(1)求证:△DEC∽△ADC;
(2)求⊙O的直径;
(3)延长AB到H,使BH=OB.求证:CH是⊙O的切线.
分析 (1)根据圆周角定理,由$\widehat{CD}$=$\widehat{BC}$得到∠CDB=∠DAC,则根据相似三角形的判定方法可判断△DEC∽△ADC;
(2)由△DEC∽△ADC,利用相似比可计算出CD=$\sqrt{3}$,再证明△DEC∽△BEA,然后利用相似比可计算出AB=2$\sqrt{3}$;
(3)连结OC,如图,根据圆周角定理得到∠ACB=90°,再利用正弦定义可求出∠ABC=60°,则△OBC为等边三角形,所以BC=OB,于是有BC=BH=BO,则可判断△OCB为直角三角形,即∠OCH=90°,然后根据切线的判定定理即可得到结论.
解答 (1)证明:∵C是劣弧$\widehat{BD}$的中点,
∴$\widehat{CD}$=$\widehat{BC}$,
∴∠CDB=∠DAC,
而∠DCE=∠ACD,
∴△DEC∽△ADC;
(2)解:∵△DEC∽△ADC,
∴CD:AC=CE:CD,即CD:3=1:CD,
∴CD=$\sqrt{3}$,
∵∠BDC=∠BAC,∠DCA=∠DBA,
∴△DEC∽△BEA,
∴CD:AB=CE:AE,即$\sqrt{3}$:AB=1:2,
∴AB=2$\sqrt{3}$,
即⊙O的直径为2$\sqrt{3}$;
(3)证明:连结OC,如图,
∵AB为直径,
∴∠ACB=90°,
∵sin∠ABC=$\frac{AC}{AB}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠ABC=60°,
∴△OBC为等边三角形,
∴BC=OB,
而BH=OB,
∴BC=BH=BO,
∴△OCB为直角三角形,即∠OCH=90°,
∴OC⊥CH,
∴CH是⊙O的切线.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线;要证某线是圆的∠切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

 如图,有两个全等的正方形ABCD和BEFC,则tan(∠BAF+∠AFB)等于( )
如图,有两个全等的正方形ABCD和BEFC,则tan(∠BAF+∠AFB)等于( )| A. | 1 | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\sqrt{2}$ |
 如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )
如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AD=10,BC=5,则∠D等于( )| A. | 150° | B. | 60° | C. | 45° | D. | 30° |

 如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点,过点P作PE⊥AB交AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF为等腰三角形时,AP的长为2或$\sqrt{2}$+1或2$\sqrt{2}$.
如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点,过点P作PE⊥AB交AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF为等腰三角形时,AP的长为2或$\sqrt{2}$+1或2$\sqrt{2}$.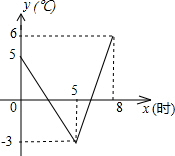 由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,某种植物在气温是0℃以下的时间超过3小时,即遭受霜冻灾害,需采取预防措施.下图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.根据图中信息:
由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”,某种植物在气温是0℃以下的时间超过3小时,即遭受霜冻灾害,需采取预防措施.下图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.根据图中信息: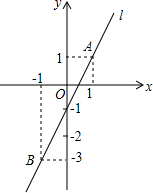 如图,已知直线l经过点A(1,1)和点B(-1,-3).试求:
如图,已知直线l经过点A(1,1)和点B(-1,-3).试求: