题目内容
11.如图,A、B、C、D、E五点共线,且AC=$\frac{1}{2}$CD,E为BD的中点,DE=$\frac{1}{5}$AB=4,求CE的长.
分析 先根据DE=$\frac{1}{5}$AB=4求出AB的长,再根据E为BD的中点求出BD的长,进而得出AD的长,再根据AC=$\frac{1}{2}$CD可求出CD的长,由CE=CD+DE即可得出结论.
解答 解:∵DE=$\frac{1}{5}$AB=4,
∴AB=4×5=20,
∵E为BD的中点,
∴BD=2DE=2×4=8,
∴AD=AB-BD=20-8=12,
∵AC=$\frac{1}{2}$CD,
∴CD=$\frac{2}{3}$AD=$\frac{2}{3}$×12=8,
∴CE=CD+DE=8+4=12.
点评 本题考查的是两点间的距离,熟知各线段之间的倍数关系是解答此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
6.下列数组中是勾股数的是( )
| A. | 6,8,9 | B. | 7,15,17 | C. | 7,24,26 | D. | 5,12,13 |
 作图题,求作一点P,使PM=PN,且到∠AOB的两边距离也相等.
作图题,求作一点P,使PM=PN,且到∠AOB的两边距离也相等.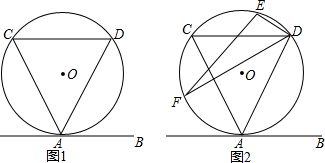
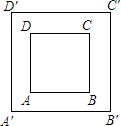 如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.
如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.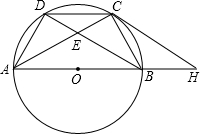 如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.
如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.