题目内容
4.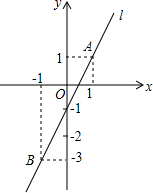 如图,已知直线l经过点A(1,1)和点B(-1,-3).试求:
如图,已知直线l经过点A(1,1)和点B(-1,-3).试求:(1)直线l的解析式;
(2)直线l与坐标轴的交点坐标;
(3)直线l与坐标轴围成的三角形面积.
分析 (1)利用待定系数求直线解析式;
(2)利用坐标轴上点的坐标特征求直线l与坐标轴的交点坐标;
(3)根据三角形面积公式求解.
解答 解:(1)设直线l的解析式为y=kx+b,
根据题意得$\left\{\begin{array}{l}{k+b=1}\\{-k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
所以直线l的解析式为y=2x-1;
(2)当x=0时,y=2x-1=-1,则直线l与y轴的交点坐标为(0,-1);
当y7=0时,2x-1=0,解得x=$\frac{1}{2}$,则直线l与x轴的交点坐标为($\frac{1}{2}$,0);
(3)直线l与坐标轴围成的三角形面积=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列各式由左边到右边的变形,是因式分解的是( )
| A. | 3x(x+y)+3x2+3xy | B. | -2x2-2xy=-2x(x+y) | C. | (x+5)(x-5)=x2-25 | D. | x2+x+1=x(x+1)+1 |
16.将分式方程$\frac{3}{x-4}$-$\frac{5-x}{4-x}$=2去分母,其中结果正确的是( )
| A. | 3+5-x=2(x-4) | B. | 3-5-x=2(4-x) | C. | 3-5-x=2(x-4) | D. | 3-5+x=-2(x-4) |
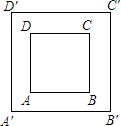 如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.
如图,有一块矩形草坪,沿草坪四周有宽为3m的环形小路.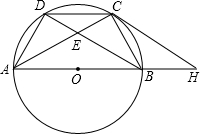 如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.
如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧$\widehat{BD}$的中点,AC交BD于点E,AE=2,EC=1.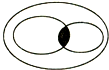 从知识结构来看,平行四边形、矩形、菱形、正方形的包含关系可以如图表示,则其中最大的椭圆表示的是平行四边形,阴影部分表示的是正方形.
从知识结构来看,平行四边形、矩形、菱形、正方形的包含关系可以如图表示,则其中最大的椭圆表示的是平行四边形,阴影部分表示的是正方形.
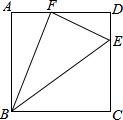 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若AB=4,AD=5,tan∠DFE=$\frac{3}{4}$,求sin∠FBE的值.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若AB=4,AD=5,tan∠DFE=$\frac{3}{4}$,求sin∠FBE的值.