题目内容
1.某商场将进价为每盒20元的商品以每盒36元售出,平均每天能售出40盒.经市场调查发现:这种商品的售价每盒每降低1元,平均每天就可以多销售10盒,要使每天的利润达到750元,并希望尽快减少库存,应将每盒的售价降低多少元?分析 利用每一盒的利润×销售的数量=获得的利润列出方程解答即可.
解答 解:设应将每盒的售价降低x元.由题意,得
(36-x-20)(40+10x)=750,
整理,得x2-12x+11=0,
解得x1=1,x2=11
∵要尽快减少库存,
∴x=1应舍去,∴x=11.
答:应将每盒的售价降低11元.
点评 此题考查一元二次方程的实际运用,掌握销售问题中的基本数量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知关于x的一元二次方程a(1+x2)+2bx=c(1-x2),其中a、b、c分别为△ABC三边的长,如果方程有两个相等的实数根,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
9.一元二次方程(x-2)(x+3)=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
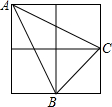 如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.
如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.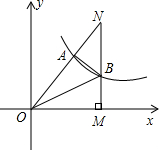 如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1).
如图,双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A,与直角边MN相交于点B,若OA=2AN,且△OAB的面积恰是方程(2-$\sqrt{3}$)x2-4($\sqrt{3}$-1)x-10=0的根,则k的值是12($\sqrt{3}$+1). 如图,已知△ABC
如图,已知△ABC