Question

6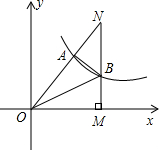．如图，双曲线y=$\frac{k}{x}$经过Rt△OMN斜边上的点A，与直角边MN相交于点B，若OA=2AN，且△OAB的面积恰是方程（2-$\sqrt{3}$）x²-4（$\sqrt{3}$-1）x-10=0的根，则k的值是12（$\sqrt{3}$+1）．

Answer 1

分析 先求出x的值，再作AC⊥x轴于点C，由OA=2AN，可设OC=2a，则CM=a，OM=3a，再根据S_△OAB=S_△AOC+S_梯形ACMB-S_△OBM即可得出结论．

解答 解：整理方程，得x²-4（$\sqrt{3}$+1）x-5（$\sqrt{3}$+1）²=0，
因式分解法解得x₁=5（$\sqrt{3}$+1），x₂=-（$\sqrt{3}$+1）舍去；
作AC⊥x轴于点C，
∵OA=2AN，
∴设OC=2a，则CM=a，OM=3a，
∴AC=$\frac{k}{2a}$，BM=$\frac{k}{3a}$，
∴S_△OAB=$\frac{1}{2}$OC×AC+$\frac{1}{2}$[AC+BM]×CM-$\frac{1}{2}$OM×BM=5（$\sqrt{3}$+1），即$\frac{1}{2}$•2a•$\frac{k}{2a}$+$\frac{1}{2}$（$\frac{k}{2a}$+$\frac{k}{3a}$）•a=5（$\sqrt{3}$+1），
解得，k=12（$\sqrt{3}$+1）．
故答案为：12（$\sqrt{3}$+1）．

点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．