题目内容
已知一个几何体的三视图都是大小相同的正方形,这个几何体是 .已知一个多项式与3x2+9x的和等于3x2+4x-1,则此多项式是 .
考点:由三视图判断几何体,整式的加减
专题:
分析:(1)依题意,一个几何体的三视图都是正方形,则只有正方体符合条件.
(2)这个多项式可表示为:(3x2+4x-1)-(3x2+9x),去括号、合并同类项即可得出答案.
(2)这个多项式可表示为:(3x2+4x-1)-(3x2+9x),去括号、合并同类项即可得出答案.
解答:解:(1)一个几何体的三视图都是大小相同的正方形,这个几何体是正方体.
(2)(3x2+4x-1)-(3x2+9x)
=3x2+4x-1-3x2-9x
=-5x-1.
故答案为:正方体,-5x-1.
(2)(3x2+4x-1)-(3x2+9x)
=3x2+4x-1-3x2-9x
=-5x-1.
故答案为:正方体,-5x-1.
点评:(1)考查由三视图确定几何体的形状,主要考查学生空间想象能力及对几何体的认识.
(2)考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.
(2)考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.

练习册系列答案
相关题目
已知抛物线y=ax2+bx+c(a>0)经过A(-1,m),B(3,m),C(-3,t),D(4,n),则( )
| A、t<n | B、t>n |
| C、t=n | D、以上均有可能 |
下列各式中,从左到右的变形是因式分解的是( )
| A、3x+3y-5=3(x+y)-5 |
| B、(x+1)(x-1)=x2-1 |
| C、x2+2x+1=(x+1)2 |
| D、x(x-y)=x2-xy |
若分式
的值为零,则x的取值应为( )
| (x-2)(x+1) |
| |x|-1 |
| A、2或-1 | B、-1 | C、2 | D、±1 |
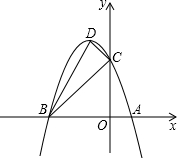 如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标
如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标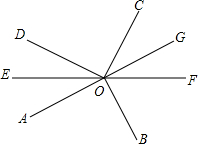 如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F. 如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.
如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.