题目内容
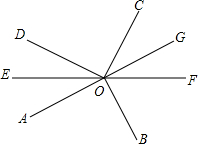 如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.(1)若∠AOD=80°,求∠BOC的度数.
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成的两个角∠COG:∠GOF=4:3,求∠AOD的度数.
考点:角平分线的定义
专题:
分析:(1)根据和等于180°的两个角互补即可求解;
(2)通过求解得到∠COF=∠BOF,根据角平分线的定义即可求解;
(3)当∠COG:∠GOF=4:3时,进行讨论即可求解.
(2)通过求解得到∠COF=∠BOF,根据角平分线的定义即可求解;
(3)当∠COG:∠GOF=4:3时,进行讨论即可求解.
解答: 解:(1)∵∠AOB=∠DOC=90°,∠AOD=80°,
解:(1)∵∠AOB=∠DOC=90°,∠AOD=80°,
∴∠BOC=360°-90°-90°-80°=100°,
(2)∵OE平分∠AOD,
∴∠EOD=∠EOA,
∴∠BOF=180°-90°-∠EOA=90°-∠EOA;
∠COF=180°-90°-∠EOD=90°-∠EOD;
∴∠BOF=∠COF,
∴射线OF是∠BOC的平分线.
(3)设∠COG=4x,∠GOF=3x,
同理可列出方程:90°+7x+4x=180°,
解得:x=
,
所以∠AOD=180-∠BOC=180-14x=
.
综上所述,∠AOD的度数是54或
.
 解:(1)∵∠AOB=∠DOC=90°,∠AOD=80°,
解:(1)∵∠AOB=∠DOC=90°,∠AOD=80°,∴∠BOC=360°-90°-90°-80°=100°,
(2)∵OE平分∠AOD,
∴∠EOD=∠EOA,
∴∠BOF=180°-90°-∠EOA=90°-∠EOA;
∠COF=180°-90°-∠EOD=90°-∠EOD;
∴∠BOF=∠COF,
∴射线OF是∠BOC的平分线.
(3)设∠COG=4x,∠GOF=3x,
同理可列出方程:90°+7x+4x=180°,
解得:x=
| 90 |
| 11 |
所以∠AOD=180-∠BOC=180-14x=
| 720 |
| 11 |
综上所述,∠AOD的度数是54或
| 720 |
| 11 |
点评:本题考查了余角和补角,角平分线的定义,同时涉及到分类思想的综合运用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
当x=1时,代数式ax3+bx+1的值为2014;则当x=-1时,ax3+bx+1的值为( )
| A、2012 | B、2015 |
| C、-2012 | D、不能确定 |
若a+b=4,ab=3,则a2-b2等于( )
| A、±8 | B、±2 | C、2 | D、8 |
计算:|3-π|的结果是( )
| A、3-π | B、3+π |
| C、π-3 | D、-(π-3) |