题目内容
下列各式中,从左到右的变形是因式分解的是( )
| A、3x+3y-5=3(x+y)-5 |
| B、(x+1)(x-1)=x2-1 |
| C、x2+2x+1=(x+1)2 |
| D、x(x-y)=x2-xy |
考点:因式分解的意义
专题:
分析:直接利用因式分解的意义分别分析得出即可.
解答:解:A、3x+3y-5=3(x+y)-5,不是分解因式,故此选项错误;
B、(x+1)(x-1)=x2-1,是整式的乘法,不是分解因式,故此选项错误;
C、x2+2x+1=(x+1)2,是分解因式,故此选项正确;
D、x(x-y)=x2-xy,是整式的乘法,不是分解因式,故此选项错误;
故选:C.
B、(x+1)(x-1)=x2-1,是整式的乘法,不是分解因式,故此选项错误;
C、x2+2x+1=(x+1)2,是分解因式,故此选项正确;
D、x(x-y)=x2-xy,是整式的乘法,不是分解因式,故此选项错误;
故选:C.
点评:此题主要考查了因式的分解的意义,正确把握定义是解题关键.

练习册系列答案
相关题目
下列现象中,可用“两点之间,线段最短”来解释的现象是( )
| A、将弯曲的河道改直,可以缩短航程 |
| B、用两个钉子就可以把木条固定在墙上 |
| C、植树时,只要先定出两棵树的位置,就能确定同一行树所在的直线 |
| D、利用圆规可以比较两条线段的长短关系 |
若a+b=4,ab=3,则a2-b2等于( )
| A、±8 | B、±2 | C、2 | D、8 |
某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可赢利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程,正确的是( )
| A、(1+50%)x-x=8 |
| B、50%x•80%-x=8 |
| C、(1+50%)x•80%=8 |
| D、(1+50%)x•80%-x=8 |
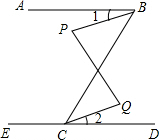 如图,已知∠ABC与∠ECB互补,∠1=∠2,判断∠P与∠Q的大小关系,并说明理由.
如图,已知∠ABC与∠ECB互补,∠1=∠2,判断∠P与∠Q的大小关系,并说明理由.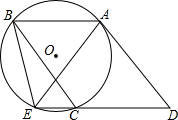 如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.
如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.