题目内容
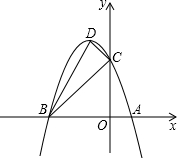 如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标
如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.坐标轴上有一动点P,使得以P、A、C为顶点的三角形与△BCD相似.则点P的坐标考点:抛物线与x轴的交点
专题:
分析:利用勾股定理求得△BCD的三边的长,然后根据勾股定理的逆定理即可作出判断,再分p在x轴和y轴两种情况讨论,舍出P的坐标,根据相似三角形的对应边的比相等即可求解.
解答: 解:过点D作DF⊥y轴于点F.
解:过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3
∴OB=OC,∴∠OCB=45°
∵在Rt△CDF中,DF=1,CF=OF-OC=4-3=1
∴DF=CF
∴∠DCF=45°
∴∠BCD=180°-∠DCF-∠OCB=90°
∴△BCD为直角三角形.
①利用△BCD的三边,
=
=
,又
=
,故当P是原点O时,△ACP∽△DBC;
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3-a,
=
,即
=
,
解得:a=-9,则P的坐标是(0,-9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3-b,则
=
,即
=
,
解得:b=-
,故P是(0,-
)时,则△ACP∽△CBD一定成立;
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1-d,当AC与CD是对应边时,
=
,即
=
,
解得:d=1-3
,此时,两个三角形不相似;
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1-e,当AC与DC是对应边时,
=
,即
=
,
解得:e=-9,符合条件.
总之,符合条件的点P的坐标为:(0,0)或(0,-
)或(-9,0).
故答案为:(0,0)或(0,-
)或(-9,0).
 解:过点D作DF⊥y轴于点F.
解:过点D作DF⊥y轴于点F.在Rt△BOC中,∵OB=3,OC=3
∴OB=OC,∴∠OCB=45°
∵在Rt△CDF中,DF=1,CF=OF-OC=4-3=1
∴DF=CF
∴∠DCF=45°
∴∠BCD=180°-∠DCF-∠OCB=90°
∴△BCD为直角三角形.
①利用△BCD的三边,
| DC |
| BC |
| ||
3
|
| 1 |
| 3 |
| OA |
| OC |
| 1 |
| 3 |
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3-a,
| AC |
| CD |
| PC |
| BD |
| ||
|
| 3-a | ||
2
|
解得:a=-9,则P的坐标是(0,-9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3-b,则
| AC |
| BC |
| PC |
| BD |
| ||
3
|
| 3-b | ||
2
|
解得:b=-
| 1 |
| 3 |
| 1 |
| 3 |
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1-d,当AC与CD是对应边时,
| AC |
| CD |
| AP |
| BC |
| ||
|
| 1-d | ||
3
|
解得:d=1-3
| 10 |
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1-e,当AC与DC是对应边时,
| AC |
| CD |
| AP |
| BD |
| ||
3
|
| 1-e | ||
2
|
解得:e=-9,符合条件.
总之,符合条件的点P的坐标为:(0,0)或(0,-
| 1 |
| 3 |
故答案为:(0,0)或(0,-
| 1 |
| 3 |
点评:此题主要考查了抛物线与x轴的交点以及勾股定理以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
计算:|3-π|的结果是( )
| A、3-π | B、3+π |
| C、π-3 | D、-(π-3) |
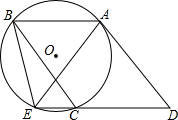 如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.
如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.